题目内容
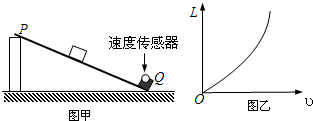
 (2011?海淀区一模)如图所示,滑板运动员从倾角为53°的斜坡顶端滑下,滑下的过程中他突然发现在斜面底端有一个高h=1.4m、宽L=1.2m的长方体障碍物,为了不触及这个障碍物,他必须距水平地面高度H=3.2m的A点沿水平方向跳起离开斜面.已知运动员的滑板与斜面间的动摩擦因数μ=0.1,忽略空气阻力,重力加速度g取10m/s2.(已知sin53°=0.8,cos53°=0.6)求:
(2011?海淀区一模)如图所示,滑板运动员从倾角为53°的斜坡顶端滑下,滑下的过程中他突然发现在斜面底端有一个高h=1.4m、宽L=1.2m的长方体障碍物,为了不触及这个障碍物,他必须距水平地面高度H=3.2m的A点沿水平方向跳起离开斜面.已知运动员的滑板与斜面间的动摩擦因数μ=0.1,忽略空气阻力,重力加速度g取10m/s2.(已知sin53°=0.8,cos53°=0.6)求:(1)运动员在斜面上滑行的加速度的大小;
(2)若运动员不触及障碍物,他从斜面上起跳后到落至水平面的过程所经历的时间;
(3)运动员为了不触及障碍物,他从A点沿水平方向起跳的最小速度.
分析:(1)运动员在斜面上滑行的过程中,受到重力、斜面的支持力和滑动摩擦力,根据牛顿第二定律求出加速度.
(2)运动员从斜面上起跳后做平抛运动,沿竖直方向做自由落体运动,由高度H求出时间.
(3)运动员为了不触及障碍物,沿水平方向起跳后竖直下落高度为H-h时,水平距离至少为Hcot53°+L,再由这两个条件求出他从A点沿水平方向起跳的最小速度.
(2)运动员从斜面上起跳后做平抛运动,沿竖直方向做自由落体运动,由高度H求出时间.
(3)运动员为了不触及障碍物,沿水平方向起跳后竖直下落高度为H-h时,水平距离至少为Hcot53°+L,再由这两个条件求出他从A点沿水平方向起跳的最小速度.
解答:解:(1)设运动员连同滑板的质量为m,运动员在斜面上滑行的过程中,根据牛顿第二定律得
mgsin53°-μmgcos53°=ma
得到运动员在斜面上滑行的加速度 a=g(sin53°-μcos53°)=7.4m/s2
(2)运动员从斜面上起跳后做平抛运动,沿竖直方向做自由落体运动,根据自由落体公式H=
gt2
解得 t=
=0.8s
(3)为了不触及障碍物,运动员以速度v沿水平方向起跳后竖直下落高度为H-h时,他沿水平方向的运动的距离为Hcot53°+L,设他在这段时间内运动的时间为t′,则 H-h=
gt′2
Hcot53°+L=vt′
解得 v=6.0m/s
答:(1)运动员在斜面上滑行的加速度的大小为7.4m/s2;
(2)若运动员不触及障碍物,他从斜面上起跳后到落至水平面的过程所经历的时间为0.8s;
(3)运动员为了不触及障碍物,他从A点沿水平方向起跳的最小速度为6.0m/s.
mgsin53°-μmgcos53°=ma
得到运动员在斜面上滑行的加速度 a=g(sin53°-μcos53°)=7.4m/s2
(2)运动员从斜面上起跳后做平抛运动,沿竖直方向做自由落体运动,根据自由落体公式H=
| 1 |
| 2 |
解得 t=
|
(3)为了不触及障碍物,运动员以速度v沿水平方向起跳后竖直下落高度为H-h时,他沿水平方向的运动的距离为Hcot53°+L,设他在这段时间内运动的时间为t′,则 H-h=
| 1 |
| 2 |
Hcot53°+L=vt′
解得 v=6.0m/s
答:(1)运动员在斜面上滑行的加速度的大小为7.4m/s2;
(2)若运动员不触及障碍物,他从斜面上起跳后到落至水平面的过程所经历的时间为0.8s;
(3)运动员为了不触及障碍物,他从A点沿水平方向起跳的最小速度为6.0m/s.
点评:本题是实际问题,考查应用物理知识解决实际问题的能力.对于平抛运动,关键分析两个方向的分位移大小.

练习册系列答案
 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
 (2011?海淀区一模)如图所示是研究平行板电容器的电容大小与哪些因素有关的实验装置.将充好电的平行板电容器与电源断开并一板接地,另一板与外壳接地的静电计相连.当改变电容器两板之间的距离和两板正对面积时,实验发现静电计指针的张角随之改变.若电容器的电容用C表示,两板之间距离用d表示,两板正对面积用S表示,静电计指针张角用θ表示.则以下对该实验现象的判断正确的是( )
(2011?海淀区一模)如图所示是研究平行板电容器的电容大小与哪些因素有关的实验装置.将充好电的平行板电容器与电源断开并一板接地,另一板与外壳接地的静电计相连.当改变电容器两板之间的距离和两板正对面积时,实验发现静电计指针的张角随之改变.若电容器的电容用C表示,两板之间距离用d表示,两板正对面积用S表示,静电计指针张角用θ表示.则以下对该实验现象的判断正确的是( )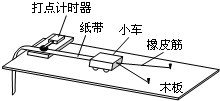 (2011?海淀区一模)(1)“探究动能定理”的实验装置如图所示,当小车在两条橡皮筋作用下弹出时,橡皮筋对小车做的功记为W0.当用4条、6条、8条…完全相同的橡皮筋并在一起进行第2次、第3次、第4次…实验时,橡皮筋对小车做的功记为2W0、3W0、4W0…,每次实验中由静止弹出的小车获得的最大速度可由打点计时器所打的纸带测出.关于该实验,下列说法正确的是
(2011?海淀区一模)(1)“探究动能定理”的实验装置如图所示,当小车在两条橡皮筋作用下弹出时,橡皮筋对小车做的功记为W0.当用4条、6条、8条…完全相同的橡皮筋并在一起进行第2次、第3次、第4次…实验时,橡皮筋对小车做的功记为2W0、3W0、4W0…,每次实验中由静止弹出的小车获得的最大速度可由打点计时器所打的纸带测出.关于该实验,下列说法正确的是