题目内容
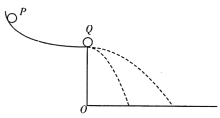
【题目】如图所示,光滑圆弧槽面末端切线水平,并静置一质量为m2的小球Q,另一质量为m1的小球P从槽面上某点由静止释放,沿槽面滑至槽口处与Q球正碰,设碰撞过程中无机械能损失,已知两球落地点到O点水平距离之比为1:2,则P、Q两球的质量之比可能是
A. 1:2 B. 2:1
C. 1:5 D. 3:5
【答案】AC
【解析】
根据平抛运动的规律得到两球碰后速度大小关系,由于碰后m1球可能沿原方向运动,也可能反弹,要分两种情况,由动量守恒定律和机械能守恒定律结合求解。
设碰前P球速度为v0,由弹性碰撞规律可知,碰后P球速度为:![]()
Q球的速度为:![]()
碰后P不反向,且落点为左侧点,又由平抛运动规律可知水平位移之比即为速度之比,则![]()
解得:![]() ,不合题意
,不合题意
碰后P反向,若左侧点为P落地点,则![]() ,解得:
,解得:![]()
若右侧点为P落地点,则![]() ,解得:
,解得:![]() ,故AC正确。
,故AC正确。
故应选:AC。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目