题目内容
 (1)某同学在做研究弹簧的形变与外力的关系实验时,将一轻弹簧竖直悬挂让其自然下垂,测出其自然长度;然后在其下部施加外力F,测出弹簧的总长度L,改变外力F的大小,测出几组数据,作出外力F与弹簧总长度L的关系图线如图所示.(实验过程是在弹簧的弹性限度内进行的)由图可知该弹簧的自然长度为
(1)某同学在做研究弹簧的形变与外力的关系实验时,将一轻弹簧竖直悬挂让其自然下垂,测出其自然长度;然后在其下部施加外力F,测出弹簧的总长度L,改变外力F的大小,测出几组数据,作出外力F与弹簧总长度L的关系图线如图所示.(实验过程是在弹簧的弹性限度内进行的)由图可知该弹簧的自然长度为10
10
cm;该弹簧的劲度系数为50
50
N/m.(2)如图所示,质量M=2
| 3 |
| 3 |
| 3 |
(1)运动过程中轻绳与水平方向夹角θ;
(2)A与水平杆间的动摩擦因数μ.
分析:(1)由图线和坐标轴交点的横坐标表示弹簧的原长可知弹簧的原长.再由胡克定律可求出弹簧的劲度系数;
(2)(1)以小球为研究对象,分析受力,作出力图,根据平衡条件求解轻绳与水平方向夹角θ;
(2)以木块和小球组成的整体为研究对象,分析受力情况,由平衡条件和摩擦力公式求木块与水平杆间的动摩擦因数μ.
(2)(1)以小球为研究对象,分析受力,作出力图,根据平衡条件求解轻绳与水平方向夹角θ;
(2)以木块和小球组成的整体为研究对象,分析受力情况,由平衡条件和摩擦力公式求木块与水平杆间的动摩擦因数μ.
解答:解:(1)当外力F大小为零时,弹簧的长度即为原长,得原长为10cm;
图线的斜率是其劲度系数,k=
=50N/m.
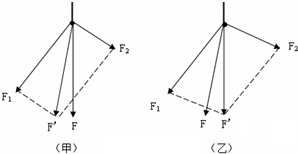
(2)(1)设轻绳对B的拉力为T,以小球为研究对象,分析受力,作出力图如图1,由平衡条件可得:

Fcos30°=Tcosθ ①
Fsin30°+Tsinθ=mg ②
解得T=10
N,tanθ=
,即θ=30°
(2)以木块和小球组成的整体为研究对象,分析受力情况,如图2.再平衡条件得
Fcos30°=f ③
N+Fsin30°=(M+m)g ④
又f=μN ⑤
解得μ=
故答案为:(1)10,50(2)30°,
.
图线的斜率是其劲度系数,k=
| △F |
| △x |
(2)(1)设轻绳对B的拉力为T,以小球为研究对象,分析受力,作出力图如图1,由平衡条件可得:

Fcos30°=Tcosθ ①
Fsin30°+Tsinθ=mg ②
解得T=10
| 3 |
| ||
| 3 |
(2)以木块和小球组成的整体为研究对象,分析受力情况,如图2.再平衡条件得
Fcos30°=f ③
N+Fsin30°=(M+m)g ④
又f=μN ⑤
解得μ=
| ||
| 5 |
故答案为:(1)10,50(2)30°,
| ||
| 5 |
点评:本题第一问关键求要会从图象中正确的找出弹簧的原长及在各外力作用下弹簧的长,并会求出弹簧的形变量,应用胡克定律求解弹簧的劲度系数;第二问关键是分别对两个物体或整体受力分析,然后运用共点力平衡条件列式求解.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目