Question

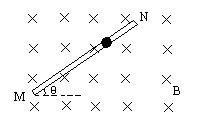
一细棒处于碰感应强度为B的匀强磁场中，棒与磁场垂直，磁感线水平向纸内，如下图所示，棒上套一个可在其上滑动的带负电的小球C，小球质量为m，电荷量为q，球与棒间动摩擦因数为μ，让小球从棒上端由静止下滑,求：

①小球的最大加速度；

②小球的最大速度；

③动摩擦因数的大小应具备什么条件？

Answer 1

答案：
解析：

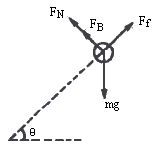
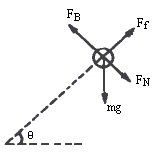
①当带电小球开始下滑后，受到重力C、洛伦兹力FB、绝缘棒的支承力FN和摩擦力Ff的作用，如下图所示． 　　随着下滑速度v增大，洛伦兹力FB(＝Bqv)增大，杆对球支承力FN减小，摩擦力Ff(＝μFN)减小，下滑加速度a(＝)增大；当支承力FN＝0时，Ff＝0，加速度a达最大值，即FN＝0(即Ff＝0)是小球具有最大加速度的临界条件，根据这个条件可得am＝gsinθ． 　　②小球达最大加速度后，虽然加速度变小，但速度还在增加，当其速度达一定值后，棒对球的压力变为斜向下，如下图所示，随着v↑→FB↑→FN↑→Ff↑→a↓，小球的加速度为零是小球具有最大速度的临界条件． 　　当a＝0时，v→vm，小球开始作匀速直线运动． 　　根据平衡条件得 　　    mgsinθ＝Ff，Ff＝μFN，mgcosθ＋FN＝Bqvm，  由此解得　　   vm＝． 　　③小球C从斜置的绝缘棒上由静止开始运动，必须满足条件 　　　　 mgsinθ＞Ff，而Ff＝μFN＝μmgcosθ， 所以应有　　   mgsinθ＞umgcosθ． 由此可得，摩擦系数μ的大小应具备条件为 　　　　　　　　 μ＜tanθ