��Ŀ����
13�� ��ͼ��ʾ��ˮƽ�����Ϸ���һ��ƽ�н������죬�����һ��Դ�������м仹����һ����K�������Ϸ���һ��������ab���ռ�����Ŵ�ֱ����ƽ�����µ���ǿ�ų�����֪��������Ϊd����Դ�綯��ΪE��������輰��Դ��������ƣ�ab���ĵ���ΪR������Ϊm�����뵼���Ħ�����ƣ��պϿ���K��ab�������˶���������ˮƽ�ɳ�����֪������ظ߶�Ϊh����������ص��ˮƽλ��Ϊs������Ľ�������ȷ��������
��ͼ��ʾ��ˮƽ�����Ϸ���һ��ƽ�н������죬�����һ��Դ�������м仹����һ����K�������Ϸ���һ��������ab���ռ�����Ŵ�ֱ����ƽ�����µ���ǿ�ų�����֪��������Ϊd����Դ�綯��ΪE��������輰��Դ��������ƣ�ab���ĵ���ΪR������Ϊm�����뵼���Ħ�����ƣ��պϿ���K��ab�������˶���������ˮƽ�ɳ�����֪������ظ߶�Ϊh����������ص��ˮƽλ��Ϊs������Ľ�������ȷ��������| A�� | ��ʼʱab���뵼���Ҷ˵ľ���L=$\frac{m{s}^{2}gR}{4h{B}^{2}{d}^{2}E}$ | |
| B�� | �ų�����ab�������Ĺ�w=$\frac{m{s}^{2}g}{8h}$ | |
| C�� | �ų�����ab���ij�����СI=ms$\sqrt{\frac{g}{2h}}$ | |
| D�� | ab���ڵ������˶�ʱ��t=$\frac{msR}{{B}^{2}{d}^{2}e}$$\sqrt{\frac{g}{2h}}$ |
���� �ɱպϵ�·ŷķ���ɿ���õ��������ɰ�������ʽ����ð�����������ab����ƽ���˶����ɿ����ab���뿪������ٶȣ��ٶ����ٹ��̷ֱ��ɶ��ܶ����Ͷ���������ʽ��⼴�ɣ�
��� �⣺A��ab�ܵ��İ�����F=BId=$\frac{BEd}{R}$��ab���뿪�������ƽ���˶���ˮƽ����s=vt����ֱ����h=$\frac{1}{2}$gt2��
��ã�v=s$\sqrt{\frac{g}{2h}}$�����ڼ��ٹ����ɶ��ܶ�����֪��
W=Fx=$\frac{1}{2}$mv2����ã�x=$\frac{m{s}^{2}gR}{4hBEd}$����A����
B������������W=$\frac{1}{2}$mv2=$\frac{m{s}^{2}g}{4h}$����B����
C���ɶ���������֪������I=mv=ms$\sqrt{\frac{g}{2h}}$����C��ȷ��
D��I=Ft�����t=$\frac{I}{F}$=$\frac{ms\sqrt{\frac{g}{2h}}}{\frac{BEd}{R}}$=$\frac{msR}{BEd}\sqrt{\frac{g}{2h}}$����D����
��ѡ��C��
���� ���⿼�鰲�������������������ܶ�����Ӧ�ã�Ҫע����ȷ�������̣���ȷ�����̶�Ӧ���������ɣ�������⣮

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ
3��һ�ҿ�ͧ��2m/s2�ļ��ٶ��ں��������ȼ���ֱ���˶�����ͧ�ij��ٶ���6m/s��8sĩʱ���ٶȴ�С�ǣ�������
| A�� | 22m/s | B�� | 16m/s | C�� | 19m/s | D�� | 48m/s |
4����ͼ��ʾ�Ľ�����ѹ����һ�������ˣ�����˵������ȷ���ǣ�������


| A�� | �ý�����ѹ��Ƶ��Ϊ50Hz | |
| B�� | �ý�����ѹ������Ϊ0.03s | |
| C�� | �����ڸõ������˵Ľ�����ѹ����ʾ��Ϊ110V | |
| D�� | �ý�����ѹ��˲ʱ����ʽΪ��=110$\sqrt{2}$sin100��t��v�� |
8���������ϵ��������ٶ�Ϊg=9.8m/�������ڳ���ϵ����ļ��ٶ�ԼΪan=3.39cm/����ʹ����ϵ����崦����ȫʧ��״̬��������ת��ӦԼΪԭ���ģ�������
| A�� | 17�� | B�� | 49�� | C�� | 98�� | D�� | 289�� |
5����ͼ����ʾ��ϸ��������һ����ȥ��������ע������ע����������ֱ���ڰڶ������ڰڶ��������ܳ�����������һϸ��īˮ��������ע�����ڶ�ƽ�洹ֱ�ķ��������϶�һ��Ӳֽ�壬�ڶ���ע����������īˮ��Ӳֽ�����γ�����ͼ����ʾ�����ߣ�ע�������쵽Ӳֽ��ľ����С���Ұڶ���ע�������ĵĸ߶ȱ仯�ɺ��Բ��ƣ�����ͼ����ʾ����xOy����ϵ����Ӳֽ���ϵ�ī�������ֵ�ͼ������Ϊע������ͼ����ͼ����ʾ��ͼ������˵������ȷ���ǣ�������


| A�� | x���ʾ�϶�Ӳֽ����ٶ� | |
| B�� | y���ʾע������λ�� | |
| C�� | �����϶�Ӳֽ���ƶ�����L��ʱ�����ע���������� | |
| D�� | �϶�Ӳֽ����ٶ�����ʹע���������ڱ�� |


 ��ͼ��ʾ���ڹ⻬��ˮƽ���Ϲ̶�����������ֱ���壬���������㹻������һ����ΪM����ΪL�ij�ľ�忿����൲�崦������һ����Ϊm��С��飨����Ϊ�ʵ㣩�������ڳ�ľ�����ˣ���֪С����볤ľ���Ķ�Ħ������Ϊ�̣���M��m����ʹС���ͳ�ľ���Թ�ͬ�ٶ�v0�����˶����賤ľ�������ҵ������ײ����е����ʧ������
��ͼ��ʾ���ڹ⻬��ˮƽ���Ϲ̶�����������ֱ���壬���������㹻������һ����ΪM����ΪL�ij�ľ�忿����൲�崦������һ����Ϊm��С��飨����Ϊ�ʵ㣩�������ڳ�ľ�����ˣ���֪С����볤ľ���Ķ�Ħ������Ϊ�̣���M��m����ʹС���ͳ�ľ���Թ�ͬ�ٶ�v0�����˶����賤ľ�������ҵ������ײ����е����ʧ������
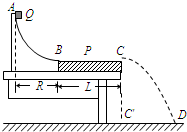 ����С���Q��ƽ��P֮��Ķ�Ħ��������ʵ��װ����ͼ��ʾ��AB�ǰ뾶�㹻��Ĺ⻬�ķ�֮һԲ���������ˮƽ�̶����õ�P����ϱ���BC��B�����У�C����ˮƽ����Ĵ�ֱͶӰΪC�䣮�������ٶ�Ϊg��ʵ�鲽�����£�
����С���Q��ƽ��P֮��Ķ�Ħ��������ʵ��װ����ͼ��ʾ��AB�ǰ뾶�㹻��Ĺ⻬�ķ�֮һԲ���������ˮƽ�̶����õ�P����ϱ���BC��B�����У�C����ˮƽ����Ĵ�ֱͶӰΪC�䣮�������ٶ�Ϊg��ʵ�鲽�����£�