题目内容
12. 如图,竖直固定轨道abcd段光滑,长为L=1.0m的平台de段粗糙,abc段是以O为圆心的圆弧.小球A和B紧靠一起静止于e处,B的质量是A的4倍.两小球在内力作用下突然分离,A分离后向左始终沿轨道运动,与de段的动摩擦因数μ=0.2,到b点时轨道对A的支持力等于A的重力的0.6,B分离后平抛落到f点,f到平台边缘的水平距离S=0.4m,平台高h=0.8m,g取10m/s2,求:
如图,竖直固定轨道abcd段光滑,长为L=1.0m的平台de段粗糙,abc段是以O为圆心的圆弧.小球A和B紧靠一起静止于e处,B的质量是A的4倍.两小球在内力作用下突然分离,A分离后向左始终沿轨道运动,与de段的动摩擦因数μ=0.2,到b点时轨道对A的支持力等于A的重力的0.6,B分离后平抛落到f点,f到平台边缘的水平距离S=0.4m,平台高h=0.8m,g取10m/s2,求:(1)AB分离时B的速度大小VB;
(2)A到达d点时的速度大小Vd;
(3)圆弧$\widehat{abc}$的半径R.
分析 (1)分离后做平抛运动,由平抛运动规律可以求得B的速度;
(2)AB分离时,由动量守恒定律列式,A球由e到d根据动能定理列式,联立方程即可求解;
(3)A球由d到b根据机械能守恒定律列式,在b点根据牛顿第二定律列式,联立方程即可求解.
解答 解:(1)B分离后做平抛运动,由平抛运动规律可知:
h=$\frac{1}{2}$gt2,vB=$\frac{s}{t}$,
代入数据得:vB=1m/s;
(2)AB分离过程系统动量守恒,以向左为正方向,由动量守恒定律得:
mAvA-mBvB=0,
A球由e到d根据动能定理得:
-μmAgl=$\frac{1}{2}$mAvd2-$\frac{1}{2}$mAve2,
代入数据得:vd=2$\sqrt{3}$m/s;
(3)A球由d到b根据机械能守恒定律得:
mAgR=$\frac{1}{2}$mAvd2-$\frac{1}{2}$mAvb2,
A球在b由牛顿第二定律得:
mAg-0.6mAg=mA$\frac{{v}_{b}^{2}}{R}$
代入数据得:R=0.5m
答:(1)AB分离时B的速度大小为1m/s;
(2)A到达d点时的速度大小为2$\sqrt{3}$m/s;
(3)圆弧$\widehat{abc}$的半径R为0.5m.
点评 本题考查了动量守恒、动能定理、机械能守恒定律等规律的直接应用,较好的考查了学生综合应用知识的能力.

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
20.一个质点做简谐振动,它的振动图象如图所示,下列判断正确的是( )


| A. | 图中的曲线部分是质点的运动轨迹 | |
| B. | 有向线段OA是质点在t1时间内的位移 | |
| C. | 振幅与有向线段OA在x轴的投影之差等于质点在t1时间内的位移大小 | |
| D. | 有向线段OA的斜率是质点在t1时刻的瞬时速率 |
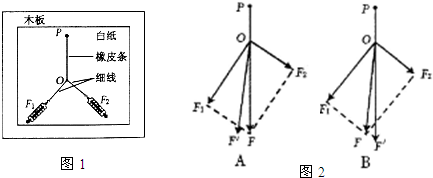
1. 一名高一学生远投篮球的照片如图所示.不计空气阻力,球出手后开始计时,在整个飞行过程中篮球受力与运动关系分析正确的是( )
一名高一学生远投篮球的照片如图所示.不计空气阻力,球出手后开始计时,在整个飞行过程中篮球受力与运动关系分析正确的是( )
 一名高一学生远投篮球的照片如图所示.不计空气阻力,球出手后开始计时,在整个飞行过程中篮球受力与运动关系分析正确的是( )
一名高一学生远投篮球的照片如图所示.不计空气阻力,球出手后开始计时,在整个飞行过程中篮球受力与运动关系分析正确的是( )| A. | 篮球受到飞行方向的推动力、重力将在空中做直线运动 | |
| B. | 篮球受到飞行方向的推动力、重力将在空中做曲线运动 | |
| C. | 篮球只受重力将在空中做匀变速运动 | |
| D. | 篮球是受重力将在空中做变速曲线运动 |
2.下列说法正确的是( )
| A. | 物体做匀速圆周运动,因向心力保持大小恒定,所以是匀变速曲线运动 | |
| B. | 圆周运动中,加速度的方向一定指向圆心 | |
| C. | 变速圆周运动中,向心力只改变速度方向 | |
| D. | 做匀速圆周运动的物体处于受力平衡状态 |
 在如图所示的电路中,电源内电阻r=2Ω,当开关S闭合后电路正常工作,电压表的读数U=8V,电流表的读数I=2A.求:
在如图所示的电路中,电源内电阻r=2Ω,当开关S闭合后电路正常工作,电压表的读数U=8V,电流表的读数I=2A.求: 如图所示,灯重G=20N,AO与天花板间夹角α=30°,BO水平,则:AO、BO两绳受到的拉力分别为40N,34.6N.
如图所示,灯重G=20N,AO与天花板间夹角α=30°,BO水平,则:AO、BO两绳受到的拉力分别为40N,34.6N.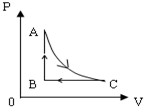 如图所示为一定质量的理想气体的P-V图线.AC段是双曲线,表示等温过程;CB段气体的温度降低(填“升高”或“降低”).
如图所示为一定质量的理想气体的P-V图线.AC段是双曲线,表示等温过程;CB段气体的温度降低(填“升高”或“降低”).