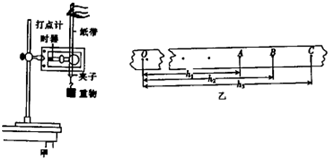
题目内容
10.在平直道路的十字路口附近,一辆长5m的货车正以v1=10m/s的速度自东向西匀速行驶,当车头距十字路口中心O的距离L1=20m时,一辆摩托车闯红灯自南向北以V2=15m/s匀速行驶,车头距中心O的距离L2=30m;为了防止撞车事故发生,摩托车紧急刹车.已知摩托车驾驶员的反应时间△t=0.5s,摩托车刹车 的加速度至少为多大时才能防止事故发生?分析 当货车整车通过中心位置,摩托车刚好到达中心位置时,此时刹车的加速度最小.根据位移公式求出货车整车通过中心位置所需的时间,根据摩托车驾驶员在反应时间内的位移,得出匀减速运动的位移,结合位移公式求出最小加速度.
解答 解:货车整车通过中心位置所需的时间为:t=$\frac{{L}_{1}+5}{{v}_{1}}=\frac{20+5}{10}s=2.5s$,
摩托车驾驶员的反应时间内的距离为:x=v2△t=15×0.5m=7.5m,
则摩托车驾驶员做匀减速运动满足:${L}_{2}-x={v}_{2}(t-△t)-\frac{1}{2}{a}_{min}(t-△t)^{2}$,
代入数据解得:${a}_{min}=3.75m/{s}^{2}$.
答:摩托车刹车的加速度至少为3.75m/s2时才能防止事故发生.
点评 本题考查了运动学中的临界问题,本题的临界情况是摩托车到达中心位置时,货车刚好整车通过中心位置,抓住时间相等,结合运动学公式灵活求解.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
1.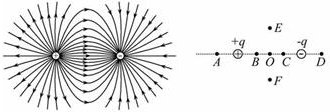 用电场线能很直观、很方便地比较电场中各点场强的强弱.如图甲是等量异种点电荷形成电场的电场线,乙图是场中的一些点:O是电荷连线的中点,E、F是连线中垂线上相对O对称的两点,B、C和A、D也相对O对称.则( )
用电场线能很直观、很方便地比较电场中各点场强的强弱.如图甲是等量异种点电荷形成电场的电场线,乙图是场中的一些点:O是电荷连线的中点,E、F是连线中垂线上相对O对称的两点,B、C和A、D也相对O对称.则( )
 用电场线能很直观、很方便地比较电场中各点场强的强弱.如图甲是等量异种点电荷形成电场的电场线,乙图是场中的一些点:O是电荷连线的中点,E、F是连线中垂线上相对O对称的两点,B、C和A、D也相对O对称.则( )
用电场线能很直观、很方便地比较电场中各点场强的强弱.如图甲是等量异种点电荷形成电场的电场线,乙图是场中的一些点:O是电荷连线的中点,E、F是连线中垂线上相对O对称的两点,B、C和A、D也相对O对称.则( )| A. | E、O、F三点比较,O点的电势最强 | B. | A、D两点场强大小相等,方向相反 | ||
| C. | E、O、F三点比较,O点的场强最强 | D. | B、O、C三点比较,O点的场强最弱 |
5. 如图所示,将一小球以v0=10m/s的水平速度抛出,抛出后小球以垂直于斜面的速度撞上倾角θ=30°的斜面,g=10m/s2,空气阻力不计,则小球从抛出到撞上斜面的时间是( )
如图所示,将一小球以v0=10m/s的水平速度抛出,抛出后小球以垂直于斜面的速度撞上倾角θ=30°的斜面,g=10m/s2,空气阻力不计,则小球从抛出到撞上斜面的时间是( )
 如图所示,将一小球以v0=10m/s的水平速度抛出,抛出后小球以垂直于斜面的速度撞上倾角θ=30°的斜面,g=10m/s2,空气阻力不计,则小球从抛出到撞上斜面的时间是( )
如图所示,将一小球以v0=10m/s的水平速度抛出,抛出后小球以垂直于斜面的速度撞上倾角θ=30°的斜面,g=10m/s2,空气阻力不计,则小球从抛出到撞上斜面的时间是( )| A. | $\frac{\sqrt{3}}{3}$s | B. | $\frac{2\sqrt{3}}{3}$s | C. | $\sqrt{3}$s | D. | 2s |
19.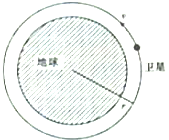 一卫星以速率v沿半径为r的圆形轨道绕地球运动,在离地心r处,地球的重力加速度为g.又物体保持匀速圆周运动的加速度为$\frac{{v}^{2}}{r}$.有四位同学试图推导出此卫星对地球的向心加速度(以g与$\frac{{v}^{2}}{r}$表示).下述选项中,正确的是( )
一卫星以速率v沿半径为r的圆形轨道绕地球运动,在离地心r处,地球的重力加速度为g.又物体保持匀速圆周运动的加速度为$\frac{{v}^{2}}{r}$.有四位同学试图推导出此卫星对地球的向心加速度(以g与$\frac{{v}^{2}}{r}$表示).下述选项中,正确的是( )
 一卫星以速率v沿半径为r的圆形轨道绕地球运动,在离地心r处,地球的重力加速度为g.又物体保持匀速圆周运动的加速度为$\frac{{v}^{2}}{r}$.有四位同学试图推导出此卫星对地球的向心加速度(以g与$\frac{{v}^{2}}{r}$表示).下述选项中,正确的是( )
一卫星以速率v沿半径为r的圆形轨道绕地球运动,在离地心r处,地球的重力加速度为g.又物体保持匀速圆周运动的加速度为$\frac{{v}^{2}}{r}$.有四位同学试图推导出此卫星对地球的向心加速度(以g与$\frac{{v}^{2}}{r}$表示).下述选项中,正确的是( )| A. | g-$\frac{{v}^{2}}{r}$=0,因为g与$\frac{{v}^{2}}{r}$等值反向 | B. | g=$\frac{{v}^{2}}{r}$,因为g即为所需的加速度$\frac{{v}^{2}}{r}$ | ||
| C. | g-$\frac{{v}^{2}}{r}$=$\frac{{v}^{2}}{r}$,因为g=$\frac{{2v}^{2}}{r}$ | D. | $\frac{{v}^{2}}{r}-g=g$,因为$\frac{{v}^{2}}{r}$=2g |
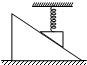 如图所示,三角物块与轻弹簧连接,静止在斜面上,轻弹簧上端固定于天花板上,呈竖直状态,则三角物块所受力的个数不可能为( )
如图所示,三角物块与轻弹簧连接,静止在斜面上,轻弹簧上端固定于天花板上,呈竖直状态,则三角物块所受力的个数不可能为( ) 如图所示,光滑$\frac{1}{4}$圆弧的半径为0.8m,有一质量为1.0kg的物体自A点从静止开始下滑到B点,然后沿水平前进4.0m,到达C点停止.g取10m/s2,求:
如图所示,光滑$\frac{1}{4}$圆弧的半径为0.8m,有一质量为1.0kg的物体自A点从静止开始下滑到B点,然后沿水平前进4.0m,到达C点停止.g取10m/s2,求: