Question

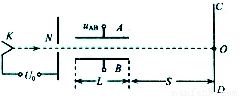
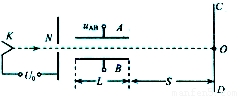
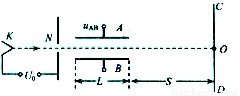
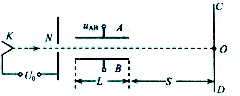如图所示是示波器的部分构造示意图，真空室中阴极K不断发出初速度可忽略的电子，电子经电压U₀=4.55×l0³V的电场加速后，由孔N沿长L=0.10m相距为d=0.020m的两平行金  属板A、B间的中心轴线进入两板间，电了穿过A、B板后最终可打在中心为O的荧光屏CD上，光屏CD距A、B板右侧距离S=0.45m．若在A、B间加U_AB=27.3V的电压．已知电子电荷最e=1.6×10^-19C，质量m=9.1×10^-31kg．求：
（1）电子通过孔N时的速度大小；
（2）荧光屏CD上的发光点距中心O的距离．

Answer 1

分析：（1）根据动能定理列式求解即可；
（2）电子的运动分为三个过程，直线加速过程，偏转过程和匀速运动过程；对于偏转过程需将其运动分解为沿水平方向和竖直方向的两个分运动研究．

解答：解：（1）设电子通过加速电场到达N孔的速度大小为v，根据动能定理，有
eU₀=

1

2

mv²
解得：
v=

2eU0 m

=

2×1.6×1019×4550 99.1×1031

=4×10⁷m/s
即电子通过孔N时的速度大小为4×10⁷m/s．
（2）设电子通过加速电场的最大偏转位移为y，由类平抛运动得
y=

1

2

eUm

md

t2
L=vt
解得：y=

11.6×1019×277.3

2×9.1×1031×0.02

(

0.1

4×107

)2=7.5×10^-4m
设荧光屏上亮线的总长度为Y．由于所有的打到荧光屏上的电子相当于从A、B板中心沿直线射出．由几何关系得

y

Y

=

L 2

S+ L 2

解得：Y=

y(2S+L)

L

=

7.5×10-4(2×0.45+0.1)

0.1

=0.0075m
即荧光屏CD上的发光点距中心O的距离为0.0075m．

点评：本题关键将电子的运动分为直线加速、电偏转和离开电场的匀速运动三个过程分析，对于类平抛运动要运用正交分解法分解为水平和竖直方向的直线运动来研究．