题目内容
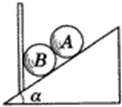如图所示，两个完全相同的光滑球A、B的质量均为m，放在竖直挡板和倾角为α的斜面间，当静止时（ ）| A、两球对斜面压力大小均为mgcosα? | ||
| B、斜面对A球的弹力大小等于mgcosα | ||
C、斜面对B球的弹力大小等于
| ||
| D、B球对A球的弹力大小等于mgsinα |
分析：以A为研究对象受力分析，根据平衡条件求斜面对A和B对A的弹力大小，进而由牛顿第三定律得出A对斜面的压力大小；
以B为研究对象受力分析，根据平衡条件列方程求斜面对B的弹力大小．
以B为研究对象受力分析，根据平衡条件列方程求斜面对B的弹力大小．
解答：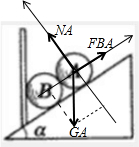
解：对A受力分析如图：
根据平衡条件：mgsinα=FBA
mgcosα=NA
故斜面对A球的弹力大小等于mgcosα，B球对A球的弹力大小等于mgsinα，故BD正确；
以B球为研究对象受力分析：
根据平衡条件：NB=mgcosα+Fsinα，根据牛顿第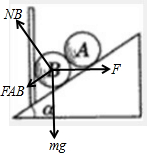
三定律B球对斜面的压力为：
mgcosα+Fsinα＞mgcosα，故A错误；
根据平衡条件，沿斜面方向：Fcosα=2mgsinα，得：F=
则NB=mgcosα+Fsinα=mgcosα+
=
故C正确；
故选：BCD．
解：对A受力分析如图：根据平衡条件：mgsinα=FBA
mgcosα=NA
故斜面对A球的弹力大小等于mgcosα，B球对A球的弹力大小等于mgsinα，故BD正确；
以B球为研究对象受力分析：
根据平衡条件：NB=mgcosα+Fsinα，根据牛顿第
三定律B球对斜面的压力为：mgcosα+Fsinα＞mgcosα，故A错误；
根据平衡条件，沿斜面方向：Fcosα=2mgsinα，得：F=
| 2mgsinα |
| cosα |
则NB=mgcosα+Fsinα=mgcosα+
| 2mgsin2α |
| cosα |
| mg(1+sin2α) |
| cosα |
故选：BCD．
点评：本题考查受力分析以及条件的应用，掌握隔离法受力分析是解决力学问题的基础．
练习册系列答案
七彩题卡口算应用一点通系列答案
相关题目
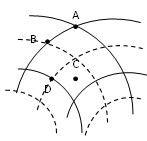
（2012?金山区一模）如图所示，两个完全相同的波源在介质中形成的波相叠加而发生的干涉的示意图，实线表示波峰，虚线表示波谷，则（ ）
（2008?上海模拟）如图所示，两个完全相同的波源在介质中形成的波相叠加而发生的干涉的示意图，实线表示波峰，虚线表示波谷，则（ ）
