题目内容
如图所示,半径为r的半圆形区域内分布着垂直纸面向里的匀强磁场,磁感应强度为B.半圆的左边分别有两平行金属网M和金属板 N,M? N两板所接电压为U,板间距离为d.现有一群质量为m?电荷量为q的带电粒子(不计重力)由静止开始从金属板 N上各处开始加速,最后均穿过磁场右边线PQ.求这些粒子到达磁场右边线PQ的最长时间和最短时间差.
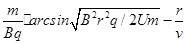
设带电粒子到达磁场边界的最短时间为t1,最长时间为t2,带电粒子进入磁场中的速度为v,由题意可判断,带电粒子沿磁场上?下两边缘运动的时间最短即等于在电场中运动的时间,即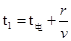
;带电粒子向着磁场的圆心射入的粒子运动时间最长等于在电场中运动的时间和在磁场中运动时间之和,即t2=t电+t磁
由动能定理得Uq=mv2/2
解得: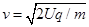
设带电粒子在磁场中运动的半径为R,则由
qvB=mv2/R
得: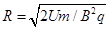
设带电粒子在磁场中做圆周运动的圆心角为θ,由几何知识得sinθ=r/R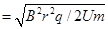
带电粒子在磁场中运动时间t磁为
t磁=θm/Bq=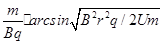
所以时间差
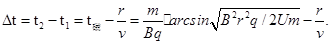
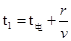;带电粒子向着磁场的圆心射入的粒子运动时间最长等于在电场中运动的时间和在磁场中运动时间之和,即t2=t电+t磁由动能定理得Uq=mv2/2
解得:
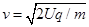
设带电粒子在磁场中运动的半径为R,则由
qvB=mv2/R
得:
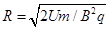
设带电粒子在磁场中做圆周运动的圆心角为θ,由几何知识得sinθ=r/R
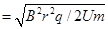
带电粒子在磁场中运动时间t磁为
t磁=θm/Bq=
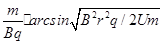
所以时间差
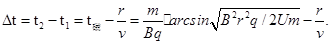
练习册系列答案
相关题目
）