题目内容
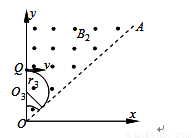
如图所示,在平行板电容器的两板之间,存在相互垂直的匀强磁场和匀强电场,磁感应强度B1=0.40T,方向垂直纸面向里,电场强度E=2.0×105V/m,PQ为板间中线.紧靠平行板右侧边缘xOy坐标系的第一象限内,有垂直纸面向外的匀强磁场,磁感应强度B2=0.25T,磁场边界AO和y轴的夹角∠AOy=45°.一束带电量q=8.0×10-19C的同位素正离子从P点射入平行板间,沿中线PQ做直线运动,穿出平行板后从y轴上坐标为(0,0.2m)的Q点垂直y轴射入磁场区,离子通过x轴时的速度方向与x轴正方向夹角在45°~90°之间,不计离子重力,求:

(1)离子运动的速度为多大?
(2)x轴上被离子打中的区间范围?
(3)离子从Q运动到x轴的最长时间?
(4)若只改变AOy区域内磁场的磁感应强度大小,使离子都不能打到x轴上,磁感应强度大小B2´应满足什么条件?
(1)5.0×105m/s(2)0.1m≤x≤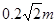 (3)
(3)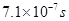 (4)B2´≥0.60T
(4)B2´≥0.60T
【解析】在有界磁场中带电粒子的运动经常涉及到临界问题,本题中带电粒子刚好穿出的临界条件就是与磁场边界相切,计算过程中的思路是先找圆心,后求半径
(1):离子在两板间时有: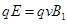 解得:v=5.0×105m/s
解得:v=5.0×105m/s
(2)当通过x轴时的速度方向与x轴正方向夹角为45°时,
到达x轴上的M点,如图所示,则:
r1=0.2m 所以:OM= 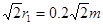
当通过x轴时的速度方向与x轴正方向夹角为90°时,
到达x轴上的N点,则:
r2=0.1m 所以:ON=r2=0.1m
所以离子到达x轴的区间范围是0.1m≤x≤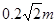
(3)所有离子速度都相同,当离子运动路程最长时,时间也最长,由图知当r=r1时离子运动时间最长,则:tm=
(4)由牛顿第二定律有: 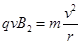 则:
则: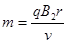
当r=r1时,同位素离子质量最大: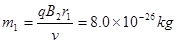
若质量最大的离子不能穿过直线OA,则所有离子必都不能到达x轴,由图可知使离子不能打到x轴上的最大半径: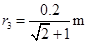
设使离子都不能打到x轴上,最小的磁感应强度大小为B0,则
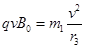
解得 B0=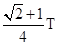 =0.60T
则:B2´≥0.60T
=0.60T
则:B2´≥0.60T

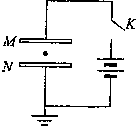
 如图所示,在平行板电容器正中有一个带电微粒.电键闭合后,该微粒恰好能保持静止.现将电键断开,能使该带电微粒向上运动打到上极板的做法是( )
如图所示,在平行板电容器正中有一个带电微粒.电键闭合后,该微粒恰好能保持静止.现将电键断开,能使该带电微粒向上运动打到上极板的做法是( ) 如图所示,在平行板电容器正中有一个带电微粒.K闭合时,该微粒恰好能保持静止.在①保持K闭合;②充电后将K断开;这两种情况下,各用什么方法能使该带电微粒向下加速运动打到下极板?( )
如图所示,在平行板电容器正中有一个带电微粒.K闭合时,该微粒恰好能保持静止.在①保持K闭合;②充电后将K断开;这两种情况下,各用什么方法能使该带电微粒向下加速运动打到下极板?( )