题目内容
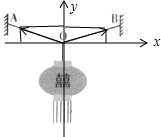
 (2010?广东)如图为节日里悬挂灯笼的一种方式,A、B点等高,O为结点,轻绳AO、BO长度相等,拉力分别为FA、FB,灯笼受到的重力为 G.下列表述正确的是( )
(2010?广东)如图为节日里悬挂灯笼的一种方式,A、B点等高,O为结点,轻绳AO、BO长度相等,拉力分别为FA、FB,灯笼受到的重力为 G.下列表述正确的是( )分析:以O点为研究对象作出受力分析图,由正交分解法可得出平行四边形,由几何关系可得出各力间的关系;
解答:解:设∠AOB=2θ,O点受到FA、FB、F三力作用,其中F=G,建立如图所示的坐标系,列平衡方程得:
FAsinθ=FBsinθ
FAcosθ+FBcosθ=G
解出:
FA=FB=
;
当θ=60°时,FA=FB=G;
当θ<60°时,FA=FB<G;
当θ>60°时,FA=FB>G;
则可知,两绳的拉力一直相等,故B正确;但F不一定小于G,故A错误;
两力的方向不在同一直线上,故不可能为平衡力,故C错误;两力可能与G相等,则两力的大小之和将大于G,故D错误;
故选B.
FAsinθ=FBsinθ
FAcosθ+FBcosθ=G
解出:
FA=FB=
| G |
| 2cosθ |
当θ=60°时,FA=FB=G;
当θ<60°时,FA=FB<G;
当θ>60°时,FA=FB>G;
则可知,两绳的拉力一直相等,故B正确;但F不一定小于G,故A错误;
两力的方向不在同一直线上,故不可能为平衡力,故C错误;两力可能与G相等,则两力的大小之和将大于G,故D错误;
故选B.

点评:本题由于两力的夹角不确定,故用合成法较为麻烦,因此本解法采用了正交分解法,可以轻松构造出直角三角形,则能顺利得出角边的关系.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
 (2010?广东)如图所示,一条轨道固定在竖直平面内,粗糙的ab段水平,bcde段光滑,cde段是以O为圆心、R为半径的一小段圆弧.可视为质点的物块A和B紧靠在一起,静止于b处,A的质量是B的3倍.两物块在足够大的内力作用下突然分离,分别向左、右始终沿轨道运动.B到b点时速度沿水平方向,此时轨道对B的支持力大小等于B所受重力的
(2010?广东)如图所示,一条轨道固定在竖直平面内,粗糙的ab段水平,bcde段光滑,cde段是以O为圆心、R为半径的一小段圆弧.可视为质点的物块A和B紧靠在一起,静止于b处,A的质量是B的3倍.两物块在足够大的内力作用下突然分离,分别向左、右始终沿轨道运动.B到b点时速度沿水平方向,此时轨道对B的支持力大小等于B所受重力的 (2010?广东)如图是密闭的气缸,外力推动活塞P压缩气体,对缸内气体做功800J,同时气体向外界放热200J,缸内气体的( )
(2010?广东)如图是密闭的气缸,外力推动活塞P压缩气体,对缸内气体做功800J,同时气体向外界放热200J,缸内气体的( ) (2010?广东)如图所示,某种自动洗衣机进水时,与洗衣缸相连的细管中会封闭一定质量的空气,通过压力传感器感知管中的空气压力,从而控制进水量.设温度不变,洗衣缸内水位升高,则细管中被封闭的空气 ( )
(2010?广东)如图所示,某种自动洗衣机进水时,与洗衣缸相连的细管中会封闭一定质量的空气,通过压力传感器感知管中的空气压力,从而控制进水量.设温度不变,洗衣缸内水位升高,则细管中被封闭的空气 ( ) (2010?广东)如图是某一点电荷的电场线分布图,下列表述正确的是( )
(2010?广东)如图是某一点电荷的电场线分布图,下列表述正确的是( )