题目内容
(10分)如图,在水平方向的匀强电场中有一表面光滑、与水平面成45°角的绝缘直杆ab,其下端(b端)距地面高度h=0.8 m.一质量为1kg的带电小环套在直杆上,正以某速度沿杆匀速下滑,小环离杆后正好通过b端的正下方c点处.(取b为零势能点,g取10 m/s2),求:
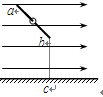
(1)小环离开直杆后运动的加速度大小和方向.
(2)小环在直杆上运动时的动能.
(3)小环从b到c运动过程中的机械能最小值.

(1)小环离开直杆后运动的加速度大小和方向.
(2)小环在直杆上运动时的动能.
(3)小环从b到c运动过程中的机械能最小值.
(1) 10 m/s2(2)2 J(3)1 J
m/s2(2)2 J(3)1 J
 m/s2(2)2 J(3)1 J
m/s2(2)2 J(3)1 J试题分析:小环在置于电场中的倾斜的光滑绝缘直杆上匀速下滑,由共点力平衡结合重力与支持力方向可判断出电场力方向,又由电场强度的方向可得出电荷的电性.当小环离 开直杆后,仅少了支持力.则此时的合力就是由重力与电场力提供,由牛顿第二定律可求出离开后的加速度大小与方向.小环离开直杆后,所受合力恰与速度方向垂 直,因此做的类平抛运动.当小环从C到P过程中,电场力做功刚好为零,动能的变化完全由重力做功引起.当求小环离开直杆的速度时,仅从离开前无法入手,而 离开后做类平抛运动,所以利用垂直于杆的方向与沿杆的方向的位移可求出小环的抛出速度.
(1)小环沿AC杆匀速下滑,受力分析小环共受3个力,可知qE=mg,
小环离开直杆后,只受重力和电场力,F合=
 mg=ma,a=
mg=ma,a= g=10
g=10 m/s2,
m/s2,方向垂直于杆向下.
(2) 环离开杆做类平抛运动:
平行杆方向匀速运动:
 h=vt,
h=vt,垂直杆方向匀加速运动:
 h=
h=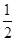 at2,
at2,由动能公式:Ek=
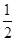 mv2
mv2解得:Ek=2 J
(3)根据能量守恒,机械能最小值E=Ek-ε
电势能:ε=
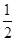 mv12
mv12v1=vcos45°
解得:E=1 J
点评:在直杆的束缚下的匀速直线运动与没有束缚下的类平抛运动.重点突出对研究对象的受力分析与运动分析,结合运动学公式、牛顿第二定律与动能定理等物理规律.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

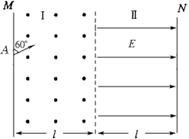
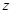 轴正方向进入匀强电场
轴正方向进入匀强电场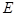 和匀强磁场
和匀强磁场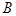 ,经偏转后打在荧光屏上
,经偏转后打在荧光屏上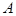 点处,则( )
点处,则( )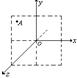
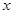 轴正方向
轴正方向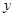 轴正方向
轴正方向
 g
g