题目内容
8．在铅球比赛中，某同学投掷铅球出手时速度大小为V0，离开地面高度h，落地的速度大小为V1，水平距离为s，铅球质量为m，投掷质量为m，投掷铅球力的大小为F，则该同学在投掷铅球时做的功为（ ）| A． | FS | B． | mgh+$\frac{1}{2}m{v}_{0}^{2}$ | C． | $\frac{1}{2}m{v}_{1}^{2}$ | D． | $\frac{1}{2}m{v}_{0}^{2}$ |
分析 根据铅球出手前后的初末动能，结合动能定理求出投掷铅球时做功的大小．
解答 解：对铅球出手前后运用动能定理得，W=$\frac{1}{2}m{{v}_{0}}^{2}-0$=$\frac{1}{2}m{{v}_{0}}^{2}$．
对整个过程研究，有：W+mgh=$\frac{1}{2}m{{v}_{1}}^{2}$，解得W=$\frac{1}{2}m{{v}_{1}}^{2}-mgh$．故D正确，A、B、C错误．
故选：D．
点评 运用动能定理解题关键选择好研究的过程，分析过程中有哪些力做功，然后根据动能定理列式求解，基础题．
练习册系列答案
相关题目
2．
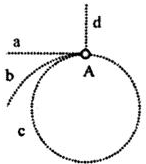如图所示，圆周c是质量为m的小球以速率v沿逆时针方向作匀速圆周运动的轨迹，轨迹圆半径为R．当小球运动到图中A点时，小球所受向心力大小突变为Fn，下列对小球随后的运动分析，其中正确的是（ ）
如图所示，圆周c是质量为m的小球以速率v沿逆时针方向作匀速圆周运动的轨迹，轨迹圆半径为R．当小球运动到图中A点时，小球所受向心力大小突变为Fn，下列对小球随后的运动分析，其中正确的是（ ）| A． | 若Fn=0，小球将沿轨迹d作匀速直线运动 | |
| B． | 若Fn＞m$\frac{{v}^{2}}{R}$，小球可能沿轨迹a作匀速直线运动 | |
| C． | 若0＜Fn＜m$\frac{{v}^{2}}{R}$，小球可能以小于v的速率沿轨迹c作圆周运动 | |
| D． | 若0＜Fn＜m$\frac{{v}^{2}}{R}$，小球可能沿轨迹b作曲线运动 |
如图所示，一滑雪爱好者（可看成质点）自上平台右端点A从静止开始沿光滑轨道滑到下平台，并从下平台右端点B水平飞出后落在水平雪面上的C点．设轨道与平台平滑连接，已知H=7.45m，h=5.00m，不计空气阻力，g取10m/s2．求：
如图所示，一条轻绳跨过同一高度上的两个轻质定滑轮，两端分别挂有质量为m1=4kg和m2=2kg的物体A和B，在定滑轮之间的一段绳上悬挂第三个物体C，O为连结点，不计滑轮的大小和摩擦，为使三个物体保持平衡，物体C的质量M应取何值？
某同学想利用滑块在倾斜气垫导轨上的运动来验证功能定理，如图所示，测量步骤如下：
13．
如图所示，物体在水平恒力F作用下，先后加速通过水平光滑水平面AB，粗糙水平面BC，已知，AB=BC，水平恒力在两个过程做的功分别为W1和W2，平均功率分别是P1和P2，则下列判断正确的是（ ）
如图所示，物体在水平恒力F作用下，先后加速通过水平光滑水平面AB，粗糙水平面BC，已知，AB=BC，水平恒力在两个过程做的功分别为W1和W2，平均功率分别是P1和P2，则下列判断正确的是（ ）| A． | W1=W2，P1＜P2 | B． | W1=W2，P1＞P2 | C． | W1＞W2，P1＞P2 | D． | W1＞W2，P1＜P2 |
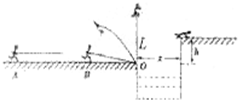如图所示，一质量m=65kg的选手参加“挑战极限运动”，要在越过宽度s=3m的水沟后跃上高h=1.8m的平台．他采用的方法是：手握长L=3.05m的轻质弹性杆一端，从A点由静止开始匀加速助跑，至B点时，杆另一端抵在O点的阻挡物上，接着杆发生形变，同时人蹬地后被弹起，到达最高点时杆处于竖直（不弯曲），人的重心恰好位于杆的顶端，此刻人放开杆水平飞出，最终落到平台上（重心恰在平台表面）．不计运动过程中的空气阻力，已知该选手匀加速运动的距离SAB=16m，到达B点时速度vB=8m/s，人跑动过程中重心离地高度H=1.0m取g=10m/s2，求选手
17．跳高运动员在如图所示的四种过杆姿势中，重心最能接近甚至低于横杆的是（ ）
| A． |  滚式 | B． |  剪式 | C． |  背越式 | D． |  跨越式 |
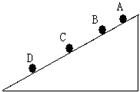相同的小球从斜面上某一位置每隔0.1s释放一个，连续放了几个后，对斜面上正在运动着的小球拍下一部分照片，如图5所示，现测得AB=15cm，BC=20cm，已知小球在斜面上做加速度相同的匀加速直线运动（初速度为零），求：