题目内容
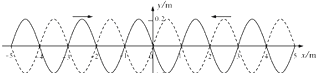 如图所示,甲、乙两列简谐横波均沿同一均质绳传播,其中甲沿正x方向传播(图中实线所示),乙沿负x方向传播(图中虚线所示).其波动频率相等且都为1Hz,振动方向均沿y轴,图示为t=0.5秒时的波形.
如图所示,甲、乙两列简谐横波均沿同一均质绳传播,其中甲沿正x方向传播(图中实线所示),乙沿负x方向传播(图中虚线所示).其波动频率相等且都为1Hz,振动方向均沿y轴,图示为t=0.5秒时的波形.①甲、乙两列波的传播速度分别是v甲=
②分别写出x=0、x=0.5m处质点的振动方程
③x轴上是否有振动加强点?如有,请代出这些点来;如没有,请说出理由
分析:由图读出波长和振幅,由波速公式求出周期,根据角速度和周期的关系求出角速度,从而写出振动方程,两列波的频率相等,相遇时会产生干涉,波峰与波峰相遇或波谷与波谷相遇时振动加强,振幅等于两列波振幅之和.
解答:解:①由图读出甲乙两列波的波长λ=2m,振幅为0.2m,由v=λf得:v甲=v乙=2×1=2m/s
②根据ω=2πf得:ω=2π×1=2πrad/s
x=0处是振动加强点,振幅A=0.2+0.2=0.4m,所以x=0处,质点的振动方程为y=0.5sin2πt m
x=0.5m处始终是振动减弱点,振幅为零,总处于平衡位移,振动方程x=0
③两列波的频率相等,相遇时会产生干涉,波峰与波峰相遇或波谷与波谷相遇时振动加强,振幅等于两列波振幅之和,由图可知,它们的坐标位置是x=±n(n=0,1,2,3…)时,振动加强.
故答案为:①2;2;
②x=0点的振动方程x=0.4sin2πt m
x=0.5m点的振动方程x=0
③有,它们的坐标位置是x=±n(n=0,1,2,3…)
②根据ω=2πf得:ω=2π×1=2πrad/s
x=0处是振动加强点,振幅A=0.2+0.2=0.4m,所以x=0处,质点的振动方程为y=0.5sin2πt m
x=0.5m处始终是振动减弱点,振幅为零,总处于平衡位移,振动方程x=0
③两列波的频率相等,相遇时会产生干涉,波峰与波峰相遇或波谷与波谷相遇时振动加强,振幅等于两列波振幅之和,由图可知,它们的坐标位置是x=±n(n=0,1,2,3…)时,振动加强.
故答案为:①2;2;
②x=0点的振动方程x=0.4sin2πt m
x=0.5m点的振动方程x=0
③有,它们的坐标位置是x=±n(n=0,1,2,3…)
点评:由波动图象读出波长、求出波速和角速度是基本能力,要求同学们能根据振动图象写出振动方程,两列波的频率相等,相遇时会产生干涉,波峰与波峰相遇或波谷与波谷相遇时振动加强,振幅等于两列波振幅之和;两列波峰与波谷相遇时振幅减弱,振幅等于两列波振幅之差.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
 如图所示,甲、乙两列完全相同的横波,分别从波源A、B两点沿直线x轴相向传播,已知在t=0时的波形如图所示.若两列波的波速均为1m/s,则C、E、F、G、D5个质点中( )
如图所示,甲、乙两列完全相同的横波,分别从波源A、B两点沿直线x轴相向传播,已知在t=0时的波形如图所示.若两列波的波速均为1m/s,则C、E、F、G、D5个质点中( )| A、t=0.2s时,只有F点的位移最大 | B、t=0.2s时,E、G两点的位移最大 | C、t=0.5s时,C、F、D三点的位移最大 | D、t=0.5s时,只有F点的位移最大 |


