题目内容
静止在水平地面上的物块,质量为20kg,现在用一个大小为60N的水平推力使物块做匀加速直线运动,当物块移动9.0m时,速度达到6.0m/s.求:
(1)物块加速度的大小?
(2)物块和地面之间的动摩擦因数?(重力加速度为9.8m/s2)
(1)物块加速度的大小?
(2)物块和地面之间的动摩擦因数?(重力加速度为9.8m/s2)
分析:根据运动学公式求出物块的加速度,通过牛顿第二定律求出物体与地面间的动摩擦因数.
解答:解:(1)根据匀变速直线运动的速度位移公式得:v2=2ax
a=
=
m/s2=2m/s2.
(2)根据牛顿第二定律得:F-μmg=ma
代入数据解得:μ=0.1.
答:(1)物块的加速度大小为2m/s2.
(2)物块和地面之间的动摩擦因数为0.1.
a=
| v2 |
| 2x |
| 36 |
| 18 |
(2)根据牛顿第二定律得:F-μmg=ma
代入数据解得:μ=0.1.
答:(1)物块的加速度大小为2m/s2.
(2)物块和地面之间的动摩擦因数为0.1.
点评:加速度是联系力学和运动学的桥梁,根据运动学公式求出加速度的大小,再通过牛顿第二定律求出动摩擦因数.

练习册系列答案
相关题目
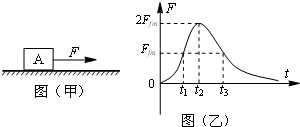 如图(甲)所示,静止在水平地面上的物块A,受到水平拉力F的作用,F与时间t的关系如图(乙)所示.设物块与地面间的最大静摩擦力Ffm的大小与滑动摩擦力大小相等,则t1~t3时间内( )
如图(甲)所示,静止在水平地面上的物块A,受到水平拉力F的作用,F与时间t的关系如图(乙)所示.设物块与地面间的最大静摩擦力Ffm的大小与滑动摩擦力大小相等,则t1~t3时间内( )| A、t1时刻物块的速度为零 | B、t2时刻物块的加速度最大 | C、t3时刻物块的动能最大 | D、t1~t3时间内F对物块先做正功后做负功 |
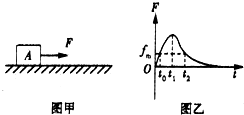 如图甲所示,静止在水平地面上的物块A,受到水平拉力F的作用,F与时间t的关系如图乙所示,设物块与地面之间的最大静摩擦力fm大小与滑动摩擦力大小相等,则下列说法中错误的是( )
如图甲所示,静止在水平地面上的物块A,受到水平拉力F的作用,F与时间t的关系如图乙所示,设物块与地面之间的最大静摩擦力fm大小与滑动摩擦力大小相等,则下列说法中错误的是( )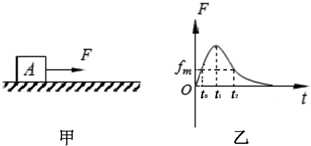
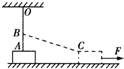 如图所示OA为遵从胡克定律的弹性轻绳,其一端固定于天花板上的0点,另一端与静止在水平地面上的物块m相连,当绳处于竖直位置时,物块m对地面有压力作用,B为紧挨绳的一光滑水平小钉,它到天花板的距离OB等于弹性绳的自然长度.现用一水平力F作用于物块m,使m向右缓慢沿直线运动,物块与地面间有摩擦,则在物块运动过程中( )
如图所示OA为遵从胡克定律的弹性轻绳,其一端固定于天花板上的0点,另一端与静止在水平地面上的物块m相连,当绳处于竖直位置时,物块m对地面有压力作用,B为紧挨绳的一光滑水平小钉,它到天花板的距离OB等于弹性绳的自然长度.现用一水平力F作用于物块m,使m向右缓慢沿直线运动,物块与地面间有摩擦,则在物块运动过程中( )