题目内容
 如图所示,圆心在O点、半径为R的光滑圆弧轨道ABC竖直固定在水平桌面上,OC与OA的夹角为60°,轨道最低点A与桌面相切.一足够长的轻绳两端分别系着质量为m1和m2的两小球D、E(均可视为质点),挂在圆弧轨道光滑边缘C的两边.开始时D位于C点,然后从静止释放.则( )
如图所示,圆心在O点、半径为R的光滑圆弧轨道ABC竖直固定在水平桌面上,OC与OA的夹角为60°,轨道最低点A与桌面相切.一足够长的轻绳两端分别系着质量为m1和m2的两小球D、E(均可视为质点),挂在圆弧轨道光滑边缘C的两边.开始时D位于C点,然后从静止释放.则( )分析:AB两个小球用绳子连在一起,说明沿绳子方向的速度是一样的,而在m1滑下去一段过程以后,此时的绳子与圆的切线是不重合,所以速度不等,重力的功率就是P=mgv,分析竖直方向速度的变化情况求解,若m1恰好能沿圆弧轨道下滑到a点,此时两小球速度均为零,根据动能定理求解做功的大小.
解答:解:A、m1由C点下滑到A点的过程中,沿绳子方向的速度是一样的,在m1滑下去一段过程以后,此时的绳子与圆的切线是不重合,而是类似于圆的一根弦线而存在,
所以此时两个物体的速度必然不相同的,故A错误;
B、重力的功率就是P=mgv,这里的v是指竖直的分速度,一开始m1是由静止释放的,所以m1一开始的竖直速度也必然为零,最后运动到A点的时候,由于此时的切线是水平的,所以此时的竖直速度也是零但是在这个C到A的过程当中是肯定有竖直分速度的,所以相当于竖直速度是从无到有再到无的一个过程,也就是一个先变大后变小的过程,所以这里重力功率mgv也是先增大后减小的过程,故B正确;
C、当D球的速度恰好为0时,由动能定理可得,W拉+m1gh=0,
当W拉=-
m1gR时,h=
R,此时D球恰好下降到A点,E球上升的高度为R,
根据机械能守恒可得,m1g
R=m2gR,
所以有m1=2m2,所以C正确;
D、由于m1=2m2时,拉力做的功W拉=-
m1gR=-m2gR,所以DE质量的关系不是m1=3m2,所以D错误.
故选BC
所以此时两个物体的速度必然不相同的,故A错误;
B、重力的功率就是P=mgv,这里的v是指竖直的分速度,一开始m1是由静止释放的,所以m1一开始的竖直速度也必然为零,最后运动到A点的时候,由于此时的切线是水平的,所以此时的竖直速度也是零但是在这个C到A的过程当中是肯定有竖直分速度的,所以相当于竖直速度是从无到有再到无的一个过程,也就是一个先变大后变小的过程,所以这里重力功率mgv也是先增大后减小的过程,故B正确;
C、当D球的速度恰好为0时,由动能定理可得,W拉+m1gh=0,
当W拉=-
| 1 |
| 2 |
| 1 |
| 2 |
根据机械能守恒可得,m1g
| 1 |
| 2 |
所以有m1=2m2,所以C正确;
D、由于m1=2m2时,拉力做的功W拉=-
| 1 |
| 2 |
故选BC
点评:本题解题的关键是对两个小球运动情况的分析,知道小球做什么运动,并能结合动能定理、几何关系解题,其中C选项的计算比较难,难度较大.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
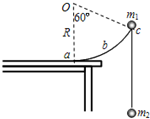 如图所示,圆心在O点、半径为R的圆弧轨道abc竖直固定在水平桌面上,Oc与Oa的夹角为60°,轨道最低点a与桌面相切.一轻绳两端系着质量为m1和m2的小球(均可视为质点),挂在圆弧轨道边缘c的两边,开始时,m1位于c点,然后从静止释放,设轻绳足够长,不计一切摩擦.则( )
如图所示,圆心在O点、半径为R的圆弧轨道abc竖直固定在水平桌面上,Oc与Oa的夹角为60°,轨道最低点a与桌面相切.一轻绳两端系着质量为m1和m2的小球(均可视为质点),挂在圆弧轨道边缘c的两边,开始时,m1位于c点,然后从静止释放,设轻绳足够长,不计一切摩擦.则( ) (2013?龙江县二模)如图所示,圆心在O点、半径为R的圆弧轨道abc竖直固定在水平桌面上,Oc与Oa的夹角为60°,轨道最低点a与桌面相切.一轻绳两端系着质量为m1和m2的小球(均可视为质点),挂在圆弧轨道边缘c的两边,开始时,m1位于c点,然后从静止释放,设轻绳足够长,不计一切摩擦.则( )
(2013?龙江县二模)如图所示,圆心在O点、半径为R的圆弧轨道abc竖直固定在水平桌面上,Oc与Oa的夹角为60°,轨道最低点a与桌面相切.一轻绳两端系着质量为m1和m2的小球(均可视为质点),挂在圆弧轨道边缘c的两边,开始时,m1位于c点,然后从静止释放,设轻绳足够长,不计一切摩擦.则( ) 如图所示,圆心在O点,半径为R=0.24m的圆弧形支架abc竖直固定在水平桌面上,支架最低点a与桌面相切,最高点c与O点的连线Oc与Oa夹角为60°.一轻绳两端系着质量分别为m1和m2的小球A和B(均可视为质点),挂在圆弧边缘c的两边.开始时,A、B均静止,A的位置与c点等高,不计一切摩擦,连线和水平桌面足够长,g=10m/s2.
如图所示,圆心在O点,半径为R=0.24m的圆弧形支架abc竖直固定在水平桌面上,支架最低点a与桌面相切,最高点c与O点的连线Oc与Oa夹角为60°.一轻绳两端系着质量分别为m1和m2的小球A和B(均可视为质点),挂在圆弧边缘c的两边.开始时,A、B均静止,A的位置与c点等高,不计一切摩擦,连线和水平桌面足够长,g=10m/s2.