题目内容
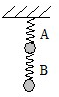
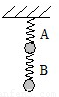
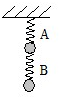 如图所示,A、B两弹簧的劲度系数均为k,两球重均为G,弹簧质量不计,下面的弹簧伸长多少,上面的弹簧伸长多少,两弹簧伸长长度之和为多少.
如图所示,A、B两弹簧的劲度系数均为k,两球重均为G,弹簧质量不计,下面的弹簧伸长多少,上面的弹簧伸长多少,两弹簧伸长长度之和为多少.分析:弹簧L1受到的弹力大小等于2G,弹簧L2受到的弹力大小等于G,根据胡克定律分别求出两根弹簧伸长的长度,再求出静止时两弹簧伸长量之和.
解答:解:B上的弹力大小为G,故B的伸长量为xB=
,而A上的弹力为2G,故A的伸长量为xA=
总伸长量为xA+xB=
答:下面的弹簧伸长
,上面的弹簧伸长
,两弹簧伸长长度之和为
.
| G |
| k |
| 2G |
| k |
总伸长量为xA+xB=
| 3G |
| k |
答:下面的弹簧伸长
| G |
| k |
| 2G |
| k |
| 3G |
| k |
点评:对于弹簧问题,关键分析弹簧的状态和弹力大小.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案
相关题目
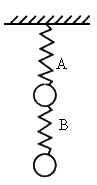

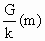
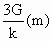
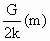
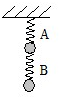 如图所示,A、B两弹簧的劲度系数均为k,两球重均为G,弹簧质量不计,下面的弹簧伸长多少,上面的弹簧伸长多少,两弹簧伸长长度之和为多少.
如图所示,A、B两弹簧的劲度系数均为k,两球重均为G,弹簧质量不计,下面的弹簧伸长多少,上面的弹簧伸长多少,两弹簧伸长长度之和为多少.