题目内容
9.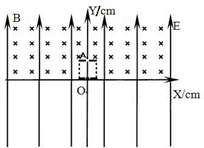 如图所示,竖直直角坐标系xoy平面内,存在方向竖直向上E=2×102V/m的匀强电场;在y>0的空间中,存在垂直xoy平面水平向里的匀强磁场,磁感应强度B=2$\sqrt{2}$×102T,一平行板电容器下极板正好在x轴上,上极板在y=5cm处,极板与y轴垂直;在y=-(5$\sqrt{2}$+5)cm处有垂直于y轴的绝缘挡板(图中未画出),小球与挡板发生弹性碰撞,碰撞遵从反射定律,有质量为m=10g、电量为q=+5×10-4C的弹性带电小球,由静止从原点出发,竖直向上经电容器两极板间电场E0=4×102V/m加速后(两极板间无磁场,极板很短),通过上极板上的小孔A进入到磁场中,g取10m/s2.试求:
如图所示,竖直直角坐标系xoy平面内,存在方向竖直向上E=2×102V/m的匀强电场;在y>0的空间中,存在垂直xoy平面水平向里的匀强磁场,磁感应强度B=2$\sqrt{2}$×102T,一平行板电容器下极板正好在x轴上,上极板在y=5cm处,极板与y轴垂直;在y=-(5$\sqrt{2}$+5)cm处有垂直于y轴的绝缘挡板(图中未画出),小球与挡板发生弹性碰撞,碰撞遵从反射定律,有质量为m=10g、电量为q=+5×10-4C的弹性带电小球,由静止从原点出发,竖直向上经电容器两极板间电场E0=4×102V/m加速后(两极板间无磁场,极板很短),通过上极板上的小孔A进入到磁场中,g取10m/s2.试求:(1)小球到达A点时的速率v0
(2)小球在磁场中运动的半径R
(3)小球从O点出发到再次回到O点所用的时间t.
分析 (1)小球在电场中加速,由动能定理可以求出小球的速度;
(2)小球在磁场中做匀速圆周运动,洛伦兹力提供向心力,由牛顿第二定律可以求出小球的轨道半径;
(3)小球在电场中加速、在磁场中做匀速圆周运动,根据匀变速运动规律与做圆周运动的周期公式求出小球的运动时间.
解答 解:(1)小球在极板间的加速过程中,
由动能定理得:$(q{E}_{0}-mg){h}_{1}=\frac{1}{2}m{v}_{0}^{2}$ …①
解得:v0=1m/s;
(2)小球在磁场中运动时,电场力平衡重力:qE=mg=0.1N …②
洛仑兹力提供小球做圆周运动的向心力,
由牛顿第二定律得:qv0B=m$\frac{{v}_{0}^{2}}{R}$ ③,
解得:R=$\frac{1}{10\sqrt{2}}$m≈0.07m=7cm ④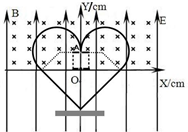
(3)小球的运动分三个阶段:
第一阶段加速直线:y=$\frac{1}{2}$$\frac{q{E}_{0}-mg}{m}$t12 …⑤
第二阶段匀速圆周,圆周运动的周期:T=$\frac{2πm}{qB}$ …⑥
圆周运动的时间:t2=$\frac{θ}{2π}$T…⑦
第三阶段匀速直线:t3=$\frac{s}{{v}_{0}}$…⑧
其中:s=$\sqrt{2}$(R+$\frac{\sqrt{2}}{2}$R)…⑨
由运动的对称性可知:t总=2(t1+t2+t3)…⑩
解得:t总=2($\frac{1}{10}$+$\frac{\sqrt{2}π}{16}$+$\frac{2+\sqrt{2}}{20}$)s≈1.098s;
答:(1)小球到达A点时的速率v0为:1m/s;
(2)小球在磁场中运动的半径R为7cm;
(3)小球从O点出发到再次回到O点所用的时间t为1.098s.
点评 本题考查了带电小球在电场与复合场中的运动,分析清楚小球的运动过程、作出小球的运动轨迹是正确解题的关键,对小球正确受力分析,应用动能定理、运动学公式与牛顿第二定律可以解题.

 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案| A. | 物体挂在弹簧秤下,弹簧秤的示数一定等于物体的重力 | |
| B. | 物体所受重力的方向都相同 | |
| C. | 用细线将物体悬挂起来,静止时物体的重心一定在悬线所在的直线上 | |
| D. | 重心就是物体所受重力的等效作用点,故重心一定在物体上 |
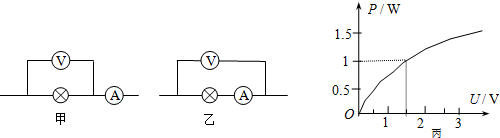
 一电荷量为q(q>0)、质量为m的带电粒子在匀强电场的作用下,在t=0时由静止开始运动,场强随时间变化的规律如图所示.不计重力,以初始电场的方向为正方向,则在t=0到t=T的时间间隔内( )
一电荷量为q(q>0)、质量为m的带电粒子在匀强电场的作用下,在t=0时由静止开始运动,场强随时间变化的规律如图所示.不计重力,以初始电场的方向为正方向,则在t=0到t=T的时间间隔内( )| A. | 粒子时而向正方向运动,时而向负方向运动 | |
| B. | 粒子一直沿正方向运动 | |
| C. | 这段时间内粒子的位移大小为$\frac{q{E}_{0}}{16m}$T2,方向沿正方向 | |
| D. | 这段时间内粒子沿反方向运动的时间为$\frac{T}{4}$ |
 如下图所示是某同学练习使用打点计时器时得到的一条纸带,并在纸带上取了四个计数点A,B,C,D,且相邻两个计数点间有四个打印点未画出.测出AB=1.2cm,AC=3.6cm,AD=7.2cm.则打B点时纸带的速度vB=0.18m/s,打C点时纸带的速度vC=0.3m/s.若纸带是匀加速直线运动则运动的加速度a=1.2m/s2.
如下图所示是某同学练习使用打点计时器时得到的一条纸带,并在纸带上取了四个计数点A,B,C,D,且相邻两个计数点间有四个打印点未画出.测出AB=1.2cm,AC=3.6cm,AD=7.2cm.则打B点时纸带的速度vB=0.18m/s,打C点时纸带的速度vC=0.3m/s.若纸带是匀加速直线运动则运动的加速度a=1.2m/s2.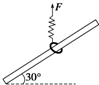 如图所示,一直杆倾斜固定,并与水平方向成30°的夹角;直杆上套有一个质量为m=0.5kg的圆环,圆环与轻弹簧相连,在轻弹簧上端施加一竖直向上、大小F=10N的力,圆环处于静止状态,已知直杆与圆环之间的动摩擦因数为μ=0.7,(g=10m/s2)
如图所示,一直杆倾斜固定,并与水平方向成30°的夹角;直杆上套有一个质量为m=0.5kg的圆环,圆环与轻弹簧相连,在轻弹簧上端施加一竖直向上、大小F=10N的力,圆环处于静止状态,已知直杆与圆环之间的动摩擦因数为μ=0.7,(g=10m/s2) 在第21届温哥华冬奥会上,我国女子冰壶队取得了优异的成绩.比赛中,冰壶在水平冰面上的运动可视为匀减速直线运动直至静止.已知一冰壶从被运动员推出的初速度大小为3m/s,其加速度大小为0.2m/s2,求:冰壶从运动到静止的过程中
在第21届温哥华冬奥会上,我国女子冰壶队取得了优异的成绩.比赛中,冰壶在水平冰面上的运动可视为匀减速直线运动直至静止.已知一冰壶从被运动员推出的初速度大小为3m/s,其加速度大小为0.2m/s2,求:冰壶从运动到静止的过程中