题目内容
3. 如图所示,水平地面上方整个空间都有水平向右的匀强电场,只在虚线右边空间存在着垂直纸面向里的匀强磁场,虚线左边有一固定的光滑水平杆,杆右端恰好与虚线重合.有一电荷量为q、质量为m的小球套在杆上并从杆左端静止释放,带电小球离开杆的右端进入正交电、磁场后,开始一小段时间内,关于小球的运动,下列说法正确的是( )
如图所示,水平地面上方整个空间都有水平向右的匀强电场,只在虚线右边空间存在着垂直纸面向里的匀强磁场,虚线左边有一固定的光滑水平杆,杆右端恰好与虚线重合.有一电荷量为q、质量为m的小球套在杆上并从杆左端静止释放,带电小球离开杆的右端进入正交电、磁场后,开始一小段时间内,关于小球的运动,下列说法正确的是( )| A. | 可能做匀速直线运动 | B. | 一定做变加速曲线运动 | ||
| C. | 重力势能可能减小 | D. | 重力势能可能增加 |
分析 首先要对小球刚进入三场的复合场时进行受力分析,通过对重力和洛伦兹力大小的无法确定上,判断小球可能上偏,也可能下偏,无论上偏还是下偏,电场力和重力都会对小球做功,可判断小球做变加速曲线运动.
解答 解:
小球加速(可判断小球带正电)后以一定的速度进入右侧电场、磁场和重力场的复合场区域,受到竖直向下的重力、竖直向上洛伦兹力和水平向右的电场力作用,如图所示.由于洛伦兹力和重力的大小关系不能确定,所以小球可能向上偏,也可能向下偏,电场力和重力做功,速率发生变化,洛伦兹力就发生变化,所以小球的合力是变力,小球做变加速曲线运动,重力势能可能增加,也可能减小.所以选项A错误,选项BCD正确.
故选:BCD.
点评 关于带电粒子在复合场中的运动注意以下几点:
复合场
(1).指电场、磁场和重力场并存,或其中两场并存,或分区存在.(组合场和叠加场)
(2).电场力和重力对带电体做功与路径无关,而磁场力对带电体不做功
运动分析
(1).当带电体所受合力为零时,将处于静止或匀速直线运动状态.
(2).当带电体作匀速圆周运动时,合外力提供向心力.
(3).当带电体作受合力大小与方向均变化时,将作非匀变速曲线运动.
解题方法及关键
(1).寻找突破口(程序法:顺藤摸瓜,逆向思维法:反其道而行之,)
(2).画好轨迹图(在画图的基础上特别注意运用几何知识寻找关系)
(3).巧选力学规律(力和运动的关系:根据带电粒子所受的力,运用牛顿第二定律并结合运动学规律求解.功能关系:根据场力及其它外力对带电粒子做功引起的能量变化或全过程中的功能关系,从而可确定带电粒子的运动情况,这条线索不但适用于均匀场,也适用于非均匀场.因此要熟悉各种力做功的特点.在解决带电粒子在复合场中的运动问题时,正确分析带电粒子的受力情况及运动特征是解题的前提,灵活选用力学规律是解题的关键.解决这类题时一定要注意临界条件的挖掘:如“恰好”、“最大”、“最多”、“至少”…等关键词,往往是解题的突破口.)

 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案 如图所示,物体在水平恒力F作用下,先后加速通过水平光滑水平面AB,粗糙水平面BC,已知,AB=BC,水平恒力在两个过程做的功分别为W1和W2,平均功率分别是P1和P2,则下列判断正确的是( )
如图所示,物体在水平恒力F作用下,先后加速通过水平光滑水平面AB,粗糙水平面BC,已知,AB=BC,水平恒力在两个过程做的功分别为W1和W2,平均功率分别是P1和P2,则下列判断正确的是( )| A. | W1=W2,P1<P2 | B. | W1=W2,P1>P2 | C. | W1>W2,P1>P2 | D. | W1>W2,P1<P2 |
| A. | 物体运动的快慢 | B. | 物体增加的速度 | ||
| C. | 物速度变化的大小 | D. | 物体速度变化的快慢 |
 如图所示,把质量为m的物体轻轻放上水平向右传送的匀速传送带,则物体刚放上时受到的摩擦力情况是( )
如图所示,把质量为m的物体轻轻放上水平向右传送的匀速传送带,则物体刚放上时受到的摩擦力情况是( )| A. | 刚放上时,物体受到水平向右的静摩擦力 | |
| B. | 刚放上时,物体受到水平向右的滑动摩擦力 | |
| C. | 刚放上时,物体受到水平向左的静摩擦力 | |
| D. | 刚放上时,物体受到水平向左的滑动摩擦力 |
 如图1,A、B是电场中的同一条直线形电场线上的两点.若将一个带负电的点电荷从A点由静止释放,它在沿电场线从A向B运动过程中的速度图象如图2所示.比较A、B两点的电势U和场强E,下列说法中正确的是( )
如图1,A、B是电场中的同一条直线形电场线上的两点.若将一个带负电的点电荷从A点由静止释放,它在沿电场线从A向B运动过程中的速度图象如图2所示.比较A、B两点的电势U和场强E,下列说法中正确的是( )| A. | UA>UB,EA>EB | B. | UA>UB,EA<EB | C. | UA<UB,EA<EB | D. | UA<UB,EA>EB |

| A. | 质点A的振幅大于质点D的振幅 | B. | 在该时刻质点D正向下运动 | ||
| C. | 在该时刻质点C、F的加速度为零 | D. | 在该时刻质点B、E的速度相同 |
| A. | 导体对电流的阻碍作用叫做导体的电阻,因此只有导体中有电流通过时才有电阻 | |
| B. | 由R=$\frac{U}{I}$可知导体的电阻与导体两端的电压成正比,跟导体中的电流成反比 | |
| C. | 将一根导线等分为二,则半根导线的电阻和电阻率都是原来的二分之一 | |
| D. | 金属材料的电阻率一般随温度的升高而增大 |
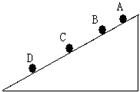 相同的小球从斜面上某一位置每隔0.1s释放一个,连续放了几个后,对斜面上正在运动着的小球拍下一部分照片,如图5所示,现测得AB=15cm,BC=20cm,已知小球在斜面上做加速度相同的匀加速直线运动(初速度为零),求:
相同的小球从斜面上某一位置每隔0.1s释放一个,连续放了几个后,对斜面上正在运动着的小球拍下一部分照片,如图5所示,现测得AB=15cm,BC=20cm,已知小球在斜面上做加速度相同的匀加速直线运动(初速度为零),求: