题目内容
12.如图所示,真空中相距为d的两块平行金属板A、B,加上电压后,产生匀强电场,所加电压波形为周期性交变电压,绝对值为U0,t=0时A板电势比B板电势高,这时靠近B板的质量为m、电量为-q的粒子开始运动(不计重力),经3.5周期后正好到达A板.求:(1)电压变化的周期T.
(2)粒子到达A板时的速度大小.

分析 粒子在两极板间先做匀加速直线运动,然后做匀减速直线运动,应用牛顿第二定律与运动学公式求出粒子的运动时间,然后求出电压变化的周期;
由匀变速直线运动的运动学公式求出粒子的速度.
解答 解:(1)粒子的加速度:a=$\frac{qE}{m}$=$\frac{q{U}_{0}}{md}$,
粒子先做匀加速运动,然后做匀减速运动,粒子的位移为:
d=3•$\frac{1}{2}$aT2+aT•$\frac{T}{2}$-$\frac{1}{2}$aT2,
解得:T=$\sqrt{\frac{2m}{3q{U}_{0}}}$d;
(2)粒子的速度为:v=aT-a$\frac{T}{2}$=$\sqrt{\frac{q{U}_{0}}{6m}}$;
答:(1)电压变化的周期T为$\sqrt{\frac{2m}{3q{U}_{0}}}$d.
(2)粒子到达A板时的速度大小为$\sqrt{\frac{q{U}_{0}}{6m}}$.
点评 本题考查了粒子的运,分析清楚粒子运动过程是正确解题的关键,应用匀变速直线运动规律可以解题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.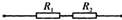 R1和R2分别标有“2Ω、1.0A”和“4Ω、0.5A”,将它们串联后接入电路中,如图所示,则此电路两端所加电压的最大值为( )
R1和R2分别标有“2Ω、1.0A”和“4Ω、0.5A”,将它们串联后接入电路中,如图所示,则此电路两端所加电压的最大值为( )
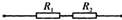 R1和R2分别标有“2Ω、1.0A”和“4Ω、0.5A”,将它们串联后接入电路中,如图所示,则此电路两端所加电压的最大值为( )
R1和R2分别标有“2Ω、1.0A”和“4Ω、0.5A”,将它们串联后接入电路中,如图所示,则此电路两端所加电压的最大值为( )| A. | 2.0 V | B. | 3.0 V | C. | 4.0 V | D. | 6 V |
20.表是一些物体运动过程中的加速度,下列对四种运动的分析比较,判断正确的是( )
| 跳伞者着陆时 | 汽车急刹车 | 汽车起步 | 列车起步 |
| -24.5m/s2 | -6m/s2 | 2m/s2 | 0.35m/s2 |
| A. | 跳伞者着陆过程的速度变化量一定最大 | |
| B. | 汽车刹车过程中,速度变化量的方向与加速度的方向相反 | |
| C. | 汽车起步过程的加速度比刹车过程的加速度小 | |
| D. | 列车起步过程速度变化最慢 |
1.质量为60kg的人,站在升降机内的台秤上,测得体重为480N,则升降机的运动可能是( )
| A. | 匀速上升 | B. | 加速下降 | C. | 减速下降 | D. | 匀速下降 |
2.关于力,速度,加速度,运动状态之间的关系,下列说法正确的是( )
| A. | 运动物体的加速度逐渐增大,速度也一定增大 | |
| B. | 物体的速度为零时,加速度也一定为零 | |
| C. | 如果物体运动状态会发生改变,则物体所受的合外力一定不为零 | |
| D. | 物体受到的合外力的方向与物体加速度方向相同,与速度方向也一定相同 |
 如图,长1.6米的滑板从斜面上由静止开始下滑,先后从标志杆A、B旁滑过,已知:滑板下滑的加速度为4m/s2,滑板经过标志杆A所用时间是0.4秒(滑板下端到达标志杆到滑板上端离开标志杆的时间),滑板经过标志杆B所用的时间是0.2秒,求:
如图,长1.6米的滑板从斜面上由静止开始下滑,先后从标志杆A、B旁滑过,已知:滑板下滑的加速度为4m/s2,滑板经过标志杆A所用时间是0.4秒(滑板下端到达标志杆到滑板上端离开标志杆的时间),滑板经过标志杆B所用的时间是0.2秒,求: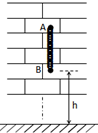 从楼房顶端使一个小球自由落下,用曝光时间为0.01s的照相机拍摄小球在空中的运动,得到的照片上有一条模糊的径迹,如图所示.照片上每块砖的厚度为6cm,径迹的下端刚好与一个已有的记号平齐,该记号与地面的高度是1.2m,小球运动到B的速度大约是多大?小球自由下落到B过程中的位移多大?楼房多高?
从楼房顶端使一个小球自由落下,用曝光时间为0.01s的照相机拍摄小球在空中的运动,得到的照片上有一条模糊的径迹,如图所示.照片上每块砖的厚度为6cm,径迹的下端刚好与一个已有的记号平齐,该记号与地面的高度是1.2m,小球运动到B的速度大约是多大?小球自由下落到B过程中的位移多大?楼房多高?