题目内容
物体A、B都静止在同一水平面上,它们的质量分别是mA、mB,与水平面间的动摩擦因数分别为μA、μB,用水平拉力F拉物体A、B,得到加速度a与拉力F关系图线如图中A、B所示,则有( )
A. B.可能有
B.可能有
C. D.
D.
C
解析试题分析:物体在水平面上运动时,受水平拉力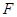 、重力
、重力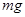 、水平面的支持力
、水平面的支持力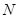 和滑动摩擦力
和滑动摩擦力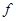 作用,根据牛顿第二定律,在水平方向上有:
作用,根据牛顿第二定律,在水平方向上有: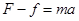 ,在竖直方向上有:
,在竖直方向上有: 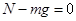 ,根据滑动摩擦定律有:
,根据滑动摩擦定律有: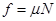 ,联立以上三式解得:
,联立以上三式解得: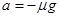 ,即a与拉力F呈一次函数关系,对照图象可知,图象中两图线的斜率关系为:
,即a与拉力F呈一次函数关系,对照图象可知,图象中两图线的斜率关系为: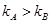 ,即:
,即: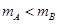 ,两图线的纵截距关系为:
,两图线的纵截距关系为: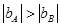 ,即:
,即: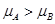 ,故选项C正确。
,故选项C正确。
考点:本题主要考查了牛顿第二定律的应用,以及分析、应用图象的能力问题,属于中档题。

 阅读快车系列答案
阅读快车系列答案如图所示,物体在一个沿斜面的拉力F的作用下,以一定的初速度沿倾角为30°的斜面向上做匀减速运动,加速度的大小为a=3 m/s2,物体在沿斜面向上的运动过程中,以下说法正确的有( )
| A.物体的机械能守恒 |
| B.物体的机械能增加 |
| C.F与摩擦力所做功的总和等于物体动能的减少量 |
| D.F与摩擦力所做功的总和等于物体机械能的增加量 |
如图所示,空间有一垂直纸面向外的磁感应强度为0.5T的匀强磁场,一质量为0.2kg,且足够长的绝缘木板静止在光滑水平面上,在木板的左端无初速放置一质量为0.1kg,电荷量q=+0.2C的滑块,滑块与绝缘木板之间动摩擦因数为0.5,滑块受到的最大静摩擦力可认为等于滑动摩擦力。现对木板施加方向水平向左,大小为0.6N的恒力,g取10m/s2。则( )
| A.木板和滑块一直以2m/s2做匀加速运动 |
| B.滑块先做匀加速运动,再做加速度减小的加速运动,最后做匀速运动 |
| C.最终木板以2m/s2做匀加速运动,滑块以10m/s做匀速运动 |
| D.最终木板以3m/s2做匀加速运动,滑块以10m/s的匀速运动 |
如图1所示,在粗糙程度处处相同的水平地面上,物块在水平向右的力F作用下由静止开始运动。运动的速度v与时间t的关系如图2所示。由图象可知,
| A.在2s—4s内,力F=0 |
| B.在4s—6s内,力F=0 |
| C.在0—2s内,力F逐渐变小 |
| D.在0—2s内,力F逐渐增大 |
质量分别为M和m的两物体靠在一起放在光滑水平面上.用水平推力F向右推M,两物体向右加速运动时,M、m间的作用力为N1;用水平力F向左推m,使M、m一起加速向左运动时,M、m间的作用力为N2,如图所示,则
| A.N1:N2=1:1 |
| B.N1:N2=m:M |
| C.N1:N2=M:m |
| D.条件不足,无法比较N1、N2的大小 |
如图甲所示,倾角为θ的光滑斜面体固定在水平面内,经度系数为k的轻弹簧,一端固定在斜面底端,另一端与质量为m的小滑块接触但不栓接,现用沿斜面向下的力F推滑块至离地高度h0处,弹簧与斜面平行,撤去力F,滑块沿斜面向上运动,其动能Ek和离地高度h的变化关系如图乙所示,图中h2对应图线的最高点,h3到h4范围内图线为直线,其余部分为曲线,重力加速度为g,则
| A.h1高度处,弹簧形变量为 |
B.h2高度处,弹簧形变量为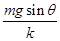 |
C.h0高度处,弹簧的弹性势能为m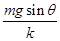 g(h3-h0) g(h3-h0) |
| D.h1高度处,弹簧的弹性势能为mg(h3-h1) |
如图所示,竖直放置的光滑圆轨道被固定在水平地面上,半径r=0.4m,最低点处有一小球(半径比r小很多),现给小球以水平向右的初速度v0,则要使小球不脱离圆轨道运动,v0应当满足(g=10m/s )()
)()
A. | B. | C. | D. |
如图所示,电梯与地面的夹角为30°,质量为m的人站在电梯上。当电梯斜向上作匀加速运动时,人对电梯的压力是他体重的1.2倍,那么,电梯的加速度a的大小和人与电梯表面间的静摩擦力f大小分别是( )
| A.a=g/2 | B.a=2g/5 |
| C.f=2mg/5 | D.f= mg/5 mg/5 |
