题目内容
 如图所示,斜面体质量为M,放在粗糙的水平面上.一滑块质量为m,放在斜面体上,由静止开始加速下滑,在滑块下滑过程中斜面体始终保持静止. 则在滑块下滑过程中( )
如图所示,斜面体质量为M,放在粗糙的水平面上.一滑块质量为m,放在斜面体上,由静止开始加速下滑,在滑块下滑过程中斜面体始终保持静止. 则在滑块下滑过程中( )分析:对整体研究:受到重力,地面的支持力和静摩擦力,作出力图.将加速度a分解为水平方向和竖直方向,根据牛顿第二定律对竖直方向进行研究求解.
解答: 解:设斜面的倾角为θ.以M和m整体为研究对象,受力图如图.
解:设斜面的倾角为θ.以M和m整体为研究对象,受力图如图.
将加速度a分解为水平方向和竖直方向,如图.
根据牛顿第二定律得
对竖直方向 (M+m)g-FN=(M+m)asinθ>0
得到FN<(M+m)g
故选B
 解:设斜面的倾角为θ.以M和m整体为研究对象,受力图如图.
解:设斜面的倾角为θ.以M和m整体为研究对象,受力图如图.将加速度a分解为水平方向和竖直方向,如图.
根据牛顿第二定律得
对竖直方向 (M+m)g-FN=(M+m)asinθ>0
得到FN<(M+m)g
故选B
点评:对于加速度不同的连接体也可以用整体法研究,这种方法中学用得不多.也可以采用隔离法分析处理.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
相关题目
 如图所示,斜面体质量为M,倾角为θ,置于水平地面上,当质量为m的小木块沿斜面体的光滑斜面自由下滑时,斜面体仍静止不动.则( )
如图所示,斜面体质量为M,倾角为θ,置于水平地面上,当质量为m的小木块沿斜面体的光滑斜面自由下滑时,斜面体仍静止不动.则( )| A、斜面体受地面的支持力等于(m+M)g | B、斜面体受地面的支持力小于(m+M)g | C、斜面体受地面的摩擦力为零 | D、斜面体受地面的摩擦力不为零 |
 如图所示,斜面体质量为M,倾角为θ,置于水平地面上,当质量为m的小木块沿斜面匀速下滑时,斜面体仍静止不动.则( )
如图所示,斜面体质量为M,倾角为θ,置于水平地面上,当质量为m的小木块沿斜面匀速下滑时,斜面体仍静止不动.则( )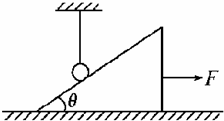 如图所示,斜面体质量为M,倾角为θ,与水平面间的动摩擦因数为μ,用细绳竖直悬挂一质量为m小球静止在光滑斜面上,当烧断绳的瞬间,至少以多大的水平向右的力由静止拉动斜面体,小球才能做自由落体运动到地面?
如图所示,斜面体质量为M,倾角为θ,与水平面间的动摩擦因数为μ,用细绳竖直悬挂一质量为m小球静止在光滑斜面上,当烧断绳的瞬间,至少以多大的水平向右的力由静止拉动斜面体,小球才能做自由落体运动到地面?