题目内容
7. 如图所示,边长为a=10cm的正方形线圈绕垂直于磁感线的OO′轴以n=10r/s的转速匀速转动,磁场的磁感应强度B=0.1T,线圈的匝数N=100匝,电阻r=1Ω.线圈两端分别接在两个固定于OO′轴上且彼此绝缘的金属滑环上,外电路接有R=9Ω的电阻,并接有一只理想交流电压表.求:
如图所示,边长为a=10cm的正方形线圈绕垂直于磁感线的OO′轴以n=10r/s的转速匀速转动,磁场的磁感应强度B=0.1T,线圈的匝数N=100匝,电阻r=1Ω.线圈两端分别接在两个固定于OO′轴上且彼此绝缘的金属滑环上,外电路接有R=9Ω的电阻,并接有一只理想交流电压表.求:(1)t=0时刻,线圈在图示位置,写出此交变电流电动势的瞬时值表达式
(2)电压表的读数;
(3)若从线圈通过中性面开始计时,转过90°过程中,通过电阻R的电荷量;
(4)在1min内,R上产生的内能Q
(5)1min内作用在线圈上的外力所做的功是多少?
分析 交流发电机产生电动势的最大值Em=nBSω,交流电压表显示的是路端电压有效值,根据$E=n\frac{△∅}{△t}$求解平均电动势,由能量守恒定律可知,外力驱动线圈所做的功将消耗的外界能量全部转化为回路中的电能,进一步转化为回路中产生的内能,能量必须用有效值计算.
解答 解:(1)从线圈从中性面位置开始计时,所求表达式应为正弦形式
e=εmsinωt=NBS2πnsinωt=100×0.1×0.01×2π×10sin(2π×10)t
得:e=2πsin20πt
(2)交流电表的读数都为有效值,电动势的有效$U=\frac{E}{R+r}R$$\frac{1}{\sqrt{2}}$=$\frac{9\sqrt{2}π}{10}$V
(3)由法拉第电磁感应定律,$E=n\frac{△∅}{△t}$ ①I=$\frac{E}{R+r}$ ②q=I△t ③
由以上三式可得:q=0.4C
(4)R上产生的内能:Q=I2Rt=$(\frac{2π}{\sqrt{2}(9+1)})^{2}×9×60$=$\frac{54\sqrt{2}}{5}{π}^{2}$J
(5)由能量守恒定律可知,外力驱动线圈所做的功将消耗的外界能量全部转化为回路中的电能,进一步转化为回路中产生的内能,能量必须用有效值计算
Q=I2(R+r)t=12π2J
答:(1)若从线圈通过中性面开始计时,线圈中交变电动势的瞬时表达式为e=2πsin20πt.
(2)电压表的读数为$\frac{9\sqrt{2}π}{10}$V.
(3)转过90°过程中,通过电阻R的电荷量为0.4C
(4)若从线圈通过中性面开始计时,转过90°过程中,平均电动势的大小为4V.
(5)在1min内,作用在线圈上的外力做功为12π2J.
点评 本题考查了交流电的峰值和有效值、周期和频率的关系,记住,求电量用电动势的平均值,求热量用有效值

 名校课堂系列答案
名校课堂系列答案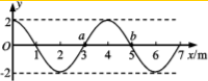
| A. | 这列波的波长为5m | |
| B. | 波中的每个质点的振动周期为4s | |
| C. | 此时质点a向下振动 | |
| D. | 若已知波速v=1m/s,则再过2s,质点a将跑到b位置 |
 一端装有定滑轮的粗糙斜面体放在地面上,A、B两物体通过细绳连接,并处于静止状态(不计绳的质量和绳与滑轮间的摩擦),如图所示.现用水平力F作用于物体B上,缓慢拉开一小角度,此过程中斜面体与物体A仍然静止.则下列说法正确的是( )
一端装有定滑轮的粗糙斜面体放在地面上,A、B两物体通过细绳连接,并处于静止状态(不计绳的质量和绳与滑轮间的摩擦),如图所示.现用水平力F作用于物体B上,缓慢拉开一小角度,此过程中斜面体与物体A仍然静止.则下列说法正确的是( )| A. | 在缓慢拉开B的过程中,水平力F不变 | |
| B. | 斜面体所受地面的支持力一定不变 | |
| C. | 斜面对物体A作用力的合力不变 | |
| D. | 斜面体受到地面的摩擦力一定变大 |
| A. | 第一宇宙速度7.9km/s是人造卫星绕地球飞行的最小速度 | |
| B. | 发射速度大于7.9km/s而小于第二宇宙速度时人造卫星将沿椭圆轨道运动 | |
| C. | 如果通信需要,地球的同步卫星可以定点在北京的上空 | |
| D. | 地球同步卫星的轨道可以是圆的,也可以是椭圆的 |
| A. | 火星公转的周期比地球公转的周期短 | |
| B. | 火星表面重力加速度约为4m/s2 | |
| C. | 火星公转的向心加速度比地球公转的向心加速度大 | |
| D. | 火星公转的线速度大于地球公转的线速度 |
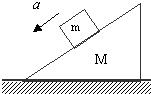 如图所示,斜面体质量为M,放在粗糙的水平面上.一滑块质量为m,放在斜面体上,由静止开始加速下滑,在滑块下滑过程中斜面体始终保持静止.则在滑块下滑过程中( )
如图所示,斜面体质量为M,放在粗糙的水平面上.一滑块质量为m,放在斜面体上,由静止开始加速下滑,在滑块下滑过程中斜面体始终保持静止.则在滑块下滑过程中( )| A. | 斜面体对地面的压力等于(M+m)g,地面对斜面体的摩擦力向左 | |
| B. | 斜面体对地面的压力小于(M+m)g,地面对斜面体的摩擦力向左 | |
| C. | 斜面体对地面的压力大于(M+m)g,地面对斜面体的摩擦力向右 | |
| D. | 斜面体对地面的压力小于(M+m)g,地面对斜面体的摩擦力向右 |
| A. | 2m/s与2m/s2 | B. | 0与4m/s2 | C. | 2m/s与4m/s2 | D. | 4m/s与0 |

| A. | 第2s末物体的加速度为零 | |
| B. | 第1s内和第2s内物体的速度方向相反 | |
| C. | 第1s内和第2s内物体的加速度方向相反 | |
| D. | 第1s内物体的速度方向与加速度方向相反 |
