题目内容
11. 如图所示,一根长0.1m的细线,一端系着一个质量为0.18kg的小球,拉住线的另一端,使小球在光滑的水平桌面上做匀速圆周运动,绳的最大张力为45N,现使小球的转速很缓慢地增加,求:
如图所示,一根长0.1m的细线,一端系着一个质量为0.18kg的小球,拉住线的另一端,使小球在光滑的水平桌面上做匀速圆周运动,绳的最大张力为45N,现使小球的转速很缓慢地增加,求:(1)线断开的瞬间,小球运动的线速度大小;
(2)如果小球离开桌面时,速度方向与桌右边缘的夹角为60°,桌面高出地面h=0.8m,求小球飞出后的落地点距桌边缘的水平距离.
分析 (1)绳的最大张力为45N,由向心力公式F=$\frac{{mv}^{2}}{r}$求出小球的速度大小.
(2)小球离开桌面后做平抛运动,由高度求出时间,并求出平抛运动的水平位移,根据所求的距离与水平位移的数学关系求解.
解答 解:(1)设线断开时小球的线速度大小为v,绳的最大张力为45N,
由FT=$\frac{{mv}^{2}}{r}$得
v=5 m/s.
(2)设桌面高度为h,小球落地经历时间为t,落地点与飞出桌面点的距离为x.
由h=$\frac{1}{2}$gt2得
t=$\sqrt{\frac{2h}{g}}$=0.4 s
x=vt=2 m
则小球飞出后的落地点到桌边缘的水平距离为l=xsin 60°=1.73 m.
答:(1)线断开的瞬间,小球运动的线速度大小是5 m/s;
(2)小球飞出后的落地点距桌边缘的水平距离是1.73 m.
点评 对于匀速圆周运动,基本方程是“指向圆心的合力”等于向心力,即F合=Fn,关键分析向心力的来源,知道小球离开桌面后做平抛运动,难度适中.

练习册系列答案
相关题目
1.根据下列提供的物理量,可以求出地球质量的是(已知万有引力常量为G)( )
| A. | 地球的半径R和月亮绕地球运转的线速度v | |
| B. | 地球绕太阳运动的周期T和公转的半径r | |
| C. | 地球表面的重力加速度g和地球的半径R | |
| D. | 月亮绕地球运转的半径r′和周期T′ |
2.关于力对物体做功,下列说法正确的是( )
| A. | 作用力的功与反作用力的功其代数和一定为零 | |
| B. | 滑动摩擦力总是做负功 | |
| C. | 静摩擦力对物体可能做正功 | |
| D. | 静摩擦力对物体一定不做功,滑动摩擦力对物体一定做功 |
6. 游乐场中的一种滑梯如图所示.小朋友从轨道顶端由静止开始下滑,沿水平轨道滑动了一段距离后停下来,则( )
游乐场中的一种滑梯如图所示.小朋友从轨道顶端由静止开始下滑,沿水平轨道滑动了一段距离后停下来,则( )
 游乐场中的一种滑梯如图所示.小朋友从轨道顶端由静止开始下滑,沿水平轨道滑动了一段距离后停下来,则( )
游乐场中的一种滑梯如图所示.小朋友从轨道顶端由静止开始下滑,沿水平轨道滑动了一段距离后停下来,则( )| A. | 下滑过程中支持力对小朋友不做功 | |
| B. | 下滑过程中小朋友的重力势能增加 | |
| C. | 整个运动过程中小朋友的机械能守恒 | |
| D. | 在水平面滑动过程中摩擦力对小朋友做负功 |
16.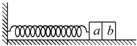 如图,一轻弹簧一端固定,另一端连接一物块构成弹簧振子,该物块是由a、b两个小物块粘在一起组成的.物块在光滑水平面上左右振动,振幅为A0,周期为T0.当物块向右通过平衡位置时,a、b之间的粘胶脱开;以后小物块a振动的振幅和周期分别为A和T,则( )
如图,一轻弹簧一端固定,另一端连接一物块构成弹簧振子,该物块是由a、b两个小物块粘在一起组成的.物块在光滑水平面上左右振动,振幅为A0,周期为T0.当物块向右通过平衡位置时,a、b之间的粘胶脱开;以后小物块a振动的振幅和周期分别为A和T,则( )
 如图,一轻弹簧一端固定,另一端连接一物块构成弹簧振子,该物块是由a、b两个小物块粘在一起组成的.物块在光滑水平面上左右振动,振幅为A0,周期为T0.当物块向右通过平衡位置时,a、b之间的粘胶脱开;以后小物块a振动的振幅和周期分别为A和T,则( )
如图,一轻弹簧一端固定,另一端连接一物块构成弹簧振子,该物块是由a、b两个小物块粘在一起组成的.物块在光滑水平面上左右振动,振幅为A0,周期为T0.当物块向右通过平衡位置时,a、b之间的粘胶脱开;以后小物块a振动的振幅和周期分别为A和T,则( )| A. | A>A0 T>T0 | B. | A>A0 T=T0 | C. | A<A0 T<T0 | D. | A>A0 T<T0 |
20.关于机械振动下列说法正确的是( )
| A. | 发生振动的条件是物体受到回复力的作用 | |
| B. | 一切往复运动都是振动 | |
| C. | 物体受周期性回复力作用时发生的振动是简谐振动 |
1.真空中有一对平行金属板,相距2.8cm,两板电势能差为32V,二价的氧离子由静止开始加速,从一个极板到另一个极板时,动能是( )
| A. | 2.8eV | B. | 5.6eV | C. | 32eV | D. | 64eV |

 某物理兴趣小组在探究平抛运动的规律实验时,分成两组,其中一个实验小组让小球做平抛运动,用频闪照相机对准方格背景照相,拍摄到如图所示的照片,已知每个小方格边长0.1m,当地的重力加速度为g=10m/s2.其中C点处的位置坐标已被污迹覆盖.
某物理兴趣小组在探究平抛运动的规律实验时,分成两组,其中一个实验小组让小球做平抛运动,用频闪照相机对准方格背景照相,拍摄到如图所示的照片,已知每个小方格边长0.1m,当地的重力加速度为g=10m/s2.其中C点处的位置坐标已被污迹覆盖.