Question

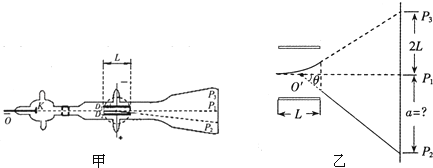
【题目】如图所示，是一儿童游戏机的工作示意图。光滑游戏面板与水平面成一夹角θ，半径为R的四分之一圆弧轨道BC与AB管道相切于B点，C点为圆弧轨道最高点，轻弹簧下端固定在AB管道的底端，上端系一轻绳，绳通过弹簧内部连一手柄P。将球投入AB管内，缓慢下拉手柄使弹簧被压缩，释放手柄，弹珠被弹出，与游戏面板内的障碍物发生一系列碰撞后落入弹槽里，根据入槽情况可以获得不同的奖励。假设所有轨道均光滑，忽略空气阻力，弹珠视为质点。某次缓慢下拉手柄，使弹珠距B点为L，释放手柄，弹珠被弹出，到达C点速度为v，下列说法正确的是
A.弹珠从释放手柄开始到触碰障碍物之前的过程中机械能不守恒
B.调整手柄的位置，可以使弹珠从C点离开后做匀变速直线运动，直到碰到障碍物
C.弹珠脱离弹簧的瞬间，其动能和重力势能之和达到最大
D.此过程中，弹簧的最大弹性势能为mg(L+R)sinθ+ mv2

Answer 1

【答案】A,C,D
【解析】因为弹珠从释放手柄的过程，弹簧对弹珠做功，其机械不守恒，故A正确；弹珠从C点离开后初速度水平向左，合力等于重力沿斜面向下的分力，两者垂直，所以弹珠做匀变速曲线运动，直到碰到障碍物，故B错误；弹珠从释放手柄的过程，弹簧的弹力对弹珠做正功，弹珠的动能和重力势能之和不断增大，根据弹珠和弹簧组成的系统机械能守恒，知弹珠脱离弹簧的瞬间，弹簧的弹性势能全部转化为弹珠的动能和重力势能，所以此瞬间动能和重力势能之和达到最大，故C正确；根据系统的机械能守恒得，弹簧的最大弹性势能等于弹珠在C点的机械能，为 ，故D正确
【考点精析】解答此题的关键在于理解功能关系的相关知识，掌握当只有重力（或弹簧弹力）做功时，物体的机械能守恒；重力对物体做的功等于物体重力势能的减少:W G =E p1 -E p2；合外力对物体所做的功等于物体动能的变化:W 合 =E k2 -E k1 （动能定理）；除了重力（或弹簧弹力）之外的力对物体所做的功等于物体机械能的变化:W F =E 2 -E 1，以及对机械能守恒及其条件的理解，了解在只有重力（和弹簧弹力）做功的情形下，物体动能和重力势能（及弹性势能）发生相互转化，但机械能的总量保持不变．