题目内容
如图所示,细绳的上端固定在天花板上靠近墙壁的O点,下端拴一小球,L点为小球下垂时的平衡位置,在OL直线上固定一个钉子Q。若将小球从竖直位置拉开(保持绳绷紧)到某位置P,释放后任其向L点摆动,不计空气阻力,小球到达L点后,因绳被钉子挡住,将开始沿以Q为中心的圆弧继续运动.下列说法正确的是( )
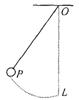
A.若Q与P等高,则小球向右摆到与P等高的点然后摆回来
B.若Q的位置比P低,则小球向右摆到与P等高的位置,然后竖直下落
C.若Q的位置比P低,则小球将绕在Q点旋转,直到绳子完全绕在钉子上为止
D.若Q的位置比P高,则小球向右能摆到与P等高的位置
AD
解析:
本题考查物体做圆周运动时向心力的供需关系及机械能守恒定律的理解和应用。当Q点比P点高或Q、P等高时,细绳始终是绷紧的,结合机械能守恒定律可知选项A、D正确;若Q点比P点低,设绳长OP=l,QL=r,![]() ,则小球能在竖直平面内做完整的圆周运动,通过圆周最高点时,需满足
,则小球能在竖直平面内做完整的圆周运动,通过圆周最高点时,需满足![]()
![]()
且![]()
可解得![]()
若![]() ,则小球运动至圆周的最高点之前的某一位置,绳子松驰,小球做针上抛运动离开圆轨道.故选项B、C错误。
,则小球运动至圆周的最高点之前的某一位置,绳子松驰,小球做针上抛运动离开圆轨道.故选项B、C错误。

练习册系列答案
相关题目
 (2010?孝感一模)如图所示,细绳的上端系在斜面的固定挡板上,下端连着物块B,轻弹簧一端与物块B相连,斜面与物块B接触处和接触处以上部分光滑(无摩擦力),斜面与物块B接触处以下部分粗糙,物块A、B的质量分别为m1、m2,物块A与斜面间的动摩擦因数为?,斜面的倾角为θ,物块A沿斜面向上滑动,刚与弹簧接触时速度大小为υ0,继续向上运动压缩弹簧并被向下弹回,物块B始终静止.弹簧的劲度系数为k,若物块A上升到最高点时细绳的拉力恰好为零.求:
(2010?孝感一模)如图所示,细绳的上端系在斜面的固定挡板上,下端连着物块B,轻弹簧一端与物块B相连,斜面与物块B接触处和接触处以上部分光滑(无摩擦力),斜面与物块B接触处以下部分粗糙,物块A、B的质量分别为m1、m2,物块A与斜面间的动摩擦因数为?,斜面的倾角为θ,物块A沿斜面向上滑动,刚与弹簧接触时速度大小为υ0,继续向上运动压缩弹簧并被向下弹回,物块B始终静止.弹簧的劲度系数为k,若物块A上升到最高点时细绳的拉力恰好为零.求: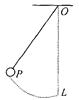

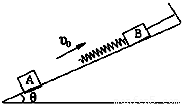 如图所示,细绳的上端系在斜面的固定挡板上,下端连着物块B,轻弹簧一端与物块B相连,斜面与物块B接触处和接触处以上部分光滑(无摩擦力),斜面与物块B接触处以下部分粗糙,物块A、B的质量分别为m1、m2,物块A与斜面间的动摩擦因数为µ,斜面的倾角为θ,物块A沿斜面向上滑动,刚与弹簧接触时速度大小为υ,继续向上运动压缩弹簧并被向下弹回,物块B始终静止.弹簧的劲度系数为k,若物块A上升到最高点时细绳的拉力恰好为零.求:
如图所示,细绳的上端系在斜面的固定挡板上,下端连着物块B,轻弹簧一端与物块B相连,斜面与物块B接触处和接触处以上部分光滑(无摩擦力),斜面与物块B接触处以下部分粗糙,物块A、B的质量分别为m1、m2,物块A与斜面间的动摩擦因数为µ,斜面的倾角为θ,物块A沿斜面向上滑动,刚与弹簧接触时速度大小为υ,继续向上运动压缩弹簧并被向下弹回,物块B始终静止.弹簧的劲度系数为k,若物块A上升到最高点时细绳的拉力恰好为零.求: