题目内容
9.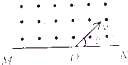 如图所示,直线MN上方存在垂直纸面向外的匀强磁场,一带电粒子(不计重力)自O点沿着与直线MN夹角为θ方向射入磁场区域,若该粒子入射速度为v时,在磁场运动的半径为R,时间为t,若该粒子入射速度为2v时,在磁场中运动的半径和时间分别为( )
如图所示,直线MN上方存在垂直纸面向外的匀强磁场,一带电粒子(不计重力)自O点沿着与直线MN夹角为θ方向射入磁场区域,若该粒子入射速度为v时,在磁场运动的半径为R,时间为t,若该粒子入射速度为2v时,在磁场中运动的半径和时间分别为( )| A. | 2R 2t | B. | 2R t | C. | R t | D. | R 2t |
分析 粒子在磁场中做匀速圆周运动,洛伦兹力提供向心力,应用牛顿第二定律求出粒子的轨道半径,根据粒子做圆周运动的周期公式与粒子转过的圆心角求出粒子的运时间.
解答 解:粒子在磁场中做匀速圆周运动,洛伦兹力提供向心力,由牛顿第二定律得:qvB=m$\frac{{v}^{2}}{R}$,
解得:R=$\frac{mv}{qB}$,
粒子轨道半径与速度成正比,当粒子速度为2v时,其轨道半径为:2R;
粒子在磁场中做圆周运动的周期:T=$\frac{2πm}{qB}$,与粒子的速度无关,
粒子速度变为2v时,粒子在磁场中转过的圆心角θ、粒子的周期T都不变,
粒子的运动时间:t=$\frac{θ}{2π}$T=$\frac{θm}{qB}$不变,仍然为t,故B正确;
故选:B.
点评 本题考查了粒子在磁场中的运动,考查了求粒子的轨道半径与运动时间,应用牛顿第二定律与粒子做圆周运动的周期公式可以解题.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
19.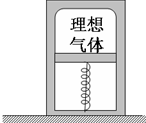 如图所示,密闭绝热的具有一定质量的活塞,活塞的上部封闭着气体,下部为真空,活塞与器壁的摩擦忽略不计,置于真空中的轻弹簧的一端固定于理想气体容器的底部.另一端固定在活塞上,弹簧被压缩后用绳扎紧,此时弹簧的弹性势能为EP(弹簧处于自然长度时的弹性势能为零),现绳突然断开,弹簧推动活塞向上运动,经过多次往复运动后活塞静止,气体达到平衡态,经过此过程( )
如图所示,密闭绝热的具有一定质量的活塞,活塞的上部封闭着气体,下部为真空,活塞与器壁的摩擦忽略不计,置于真空中的轻弹簧的一端固定于理想气体容器的底部.另一端固定在活塞上,弹簧被压缩后用绳扎紧,此时弹簧的弹性势能为EP(弹簧处于自然长度时的弹性势能为零),现绳突然断开,弹簧推动活塞向上运动,经过多次往复运动后活塞静止,气体达到平衡态,经过此过程( )
 如图所示,密闭绝热的具有一定质量的活塞,活塞的上部封闭着气体,下部为真空,活塞与器壁的摩擦忽略不计,置于真空中的轻弹簧的一端固定于理想气体容器的底部.另一端固定在活塞上,弹簧被压缩后用绳扎紧,此时弹簧的弹性势能为EP(弹簧处于自然长度时的弹性势能为零),现绳突然断开,弹簧推动活塞向上运动,经过多次往复运动后活塞静止,气体达到平衡态,经过此过程( )
如图所示,密闭绝热的具有一定质量的活塞,活塞的上部封闭着气体,下部为真空,活塞与器壁的摩擦忽略不计,置于真空中的轻弹簧的一端固定于理想气体容器的底部.另一端固定在活塞上,弹簧被压缩后用绳扎紧,此时弹簧的弹性势能为EP(弹簧处于自然长度时的弹性势能为零),现绳突然断开,弹簧推动活塞向上运动,经过多次往复运动后活塞静止,气体达到平衡态,经过此过程( )| A. | EP全部转换为气体的内能 | |
| B. | EP一部分转换成活塞的重力势能,其余部分仍为弹簧的弹性势能 | |
| C. | EP全部转换成活塞的重力势能和气体的内能 | |
| D. | EP一部分转换成活塞的重力势能,一部分转换为气体的内能,其余部分仍为弹簧的弹性势能 |
20.将杆的一端用绳子悬挂在天花板上,一端放在地面上,在图中的甲、乙、丙三种情况下,则( )

| A. | 图甲中,地面对杆的作用力的方向竖直向上 | |
| B. | 图乙中,地面受到杆的摩擦力方向向右 | |
| C. | 图丙中,地面对杆的作用力的方向一定沿杆 | |
| D. | 图丙中,杆受到地面的摩擦力方向向右 |
17.在如图所示的实验电路中,当滑动变阻器R0的滑动触头向左端滑动时( )


| A. | L1变暗,L2变亮,L3变亮 | B. | L1变暗,L2变暗,L3变亮 | ||
| C. | L1变暗,L2变暗,L3变暗 | D. | L1变亮,L2变亮,L3变暗 |
4.关于静电场下列说法正确的是( )
| A. | 负电荷沿电场线方向移动时,电势能一定增加 | |
| B. | 负电荷沿电场线方向移动时,电势能一定减小 | |
| C. | 电场强度大的位置电势一定高,电场强度小的位置电势一定低 | |
| D. | 电场强度为零的点,电势一定为零 |
14. 断开含变压器、电动机等设备的电路的开关时,开关中的金属片之间会产生电火花,电火花会烧蚀接触点,甚至引起人身伤害.关于电火花产生的原因,以下说法正确的是( )
断开含变压器、电动机等设备的电路的开关时,开关中的金属片之间会产生电火花,电火花会烧蚀接触点,甚至引起人身伤害.关于电火花产生的原因,以下说法正确的是( )
 断开含变压器、电动机等设备的电路的开关时,开关中的金属片之间会产生电火花,电火花会烧蚀接触点,甚至引起人身伤害.关于电火花产生的原因,以下说法正确的是( )
断开含变压器、电动机等设备的电路的开关时,开关中的金属片之间会产生电火花,电火花会烧蚀接触点,甚至引起人身伤害.关于电火花产生的原因,以下说法正确的是( )| A. | 断开时金属片之间摩擦起电 | |
| B. | 断开时设备中的线圈产生很大的感应电动势 | |
| C. | 由于设备正常工作时的电压很大引起的 | |
| D. | D由于设备正常工作时的电流很大引起的 |
18. 如图是牛顿研究抛体运动时绘制的一幅草图,以不同速度抛出的物体分别沿a、b、c、d轨迹运动,其中a是一段曲线,b是贴近地球表面的圆,c是椭圆,d是双曲线的一部分.已知万有引力常量G、地球质量M、半径R、地面附近的重力加速度g.以下说法正确的是( )
如图是牛顿研究抛体运动时绘制的一幅草图,以不同速度抛出的物体分别沿a、b、c、d轨迹运动,其中a是一段曲线,b是贴近地球表面的圆,c是椭圆,d是双曲线的一部分.已知万有引力常量G、地球质量M、半径R、地面附近的重力加速度g.以下说法正确的是( )
 如图是牛顿研究抛体运动时绘制的一幅草图,以不同速度抛出的物体分别沿a、b、c、d轨迹运动,其中a是一段曲线,b是贴近地球表面的圆,c是椭圆,d是双曲线的一部分.已知万有引力常量G、地球质量M、半径R、地面附近的重力加速度g.以下说法正确的是( )
如图是牛顿研究抛体运动时绘制的一幅草图,以不同速度抛出的物体分别沿a、b、c、d轨迹运动,其中a是一段曲线,b是贴近地球表面的圆,c是椭圆,d是双曲线的一部分.已知万有引力常量G、地球质量M、半径R、地面附近的重力加速度g.以下说法正确的是( )| A. | 沿a运动的物体初速度一定等于$\sqrt{gR}$ | |
| B. | 沿b运动的物体速度等于$\sqrt{\frac{GM}{R}}$ | |
| C. | 沿c运动的物体初速度一定大于第二宇宙速度 | |
| D. | 沿d运动的物体初速度一定大于第三宇宙速度 |
 如图所示,一发射器固定子啊竖直轻质圆盘边缘上,发射的时刻可人为控制,某次游戏中,圆盘以ω=4rad/s的角速度顺时针匀速转动,当发射器随圆盘转到最高点时启动发射器,发射器射出的子弹恰能射中目标,已知发射器的总质量M=2kg(不含子弹),子弹的质量为m=0.5kg,发射器能将子弹以相对于发射器v=2m/s的速度发射,圆盘半径为R=2m,目标与圆盘圆心等高,g取10m/s2.
如图所示,一发射器固定子啊竖直轻质圆盘边缘上,发射的时刻可人为控制,某次游戏中,圆盘以ω=4rad/s的角速度顺时针匀速转动,当发射器随圆盘转到最高点时启动发射器,发射器射出的子弹恰能射中目标,已知发射器的总质量M=2kg(不含子弹),子弹的质量为m=0.5kg,发射器能将子弹以相对于发射器v=2m/s的速度发射,圆盘半径为R=2m,目标与圆盘圆心等高,g取10m/s2.