题目内容
9.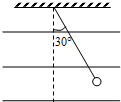 如图所示,一个质量为m=0.03kg,带电量为q=-1.0×10-8C的带电小球,用绝缘细线悬挂在某水平方向的匀强电场中,图中实线为电场线.当小球静止时,测得悬线与竖直方向成30°角.
如图所示,一个质量为m=0.03kg,带电量为q=-1.0×10-8C的带电小球,用绝缘细线悬挂在某水平方向的匀强电场中,图中实线为电场线.当小球静止时,测得悬线与竖直方向成30°角.(1)在图上标出场强的方向;
(2)该电场的场强大小为多少?
(3)若保持场强的大小不变,则将电场调整到方向能使小球保持原来的静止状态?
(4)若已知场强方向水平向左,若将该小球由竖直位置的最低点静止释放,小球运动过程中细线与竖直方向的最大偏角θ为37°,则场强大小又为多大?
(已知sin37°=0.6,cos37°=0.8)
分析 (1)由题,小球静止在电场中,受到重力、线的拉力和电场力而平衡,根据平衡条件确定小球电场力的方向,进而判断电场强度方向.
(2)小球在匀强电场中,受到的电场力大小为F=qE,根据平衡条件求出E;
(3)根据几何知识分析,运用图解法确定场强的方向.
(4)整个运动过程中根据动能定理即可求解场强的大小.
解答 解:(1)小球静止在电场中,受到重力、线的拉力和电场力而平衡,所以小球受电场力方向水平向右,而小球带负电,所以电场强度方向水平向左,如下图所示:
(2)根据平衡条件得:
tan30°=$\frac{qE}{mg}$, 解得:E=$\sqrt{3}$×107N/C
解得:E=$\sqrt{3}$×107N/C
(3)电场力qE与细线的拉力T的合力与重力等大、反向,作出T与qE的合力,如右图所示.根据几何知识得到,当电场力大小不变,方向与水平方向成60°斜向右上方,即场强方向方向与水平方向成60°斜向左上方时小球保持原来的静止状态.
(4)整个运动过程中根据动能定理得:
Eqlsin37°-mgl(1-cos37°)=0-0
解得:E=1×107N/C
答:(1)如图所示;
(2)该电场的场强大小为$\sqrt{3}$×107N/C;
(3)场强方向方向与水平方向成60°斜向左上方时小球保持原来的静止状态;
(4)若已知场强方向水平向左,若将该小球由竖直位置的最低点静止释放,小球运动过程中细线与竖直方向的最大偏角θ为37°,则场强大小为1×107N/C
点评 本题是电场中的力平衡问题,要转换观念,当作力学问题去处理.难点是运用几何知识,采用作图法确定电场力的最小值.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
20.简谐振动属于( )
| A. | 匀变速直线运动 | B. | 匀速直线运动 | C. | 曲线运动 | D. | 变速运动 |
19. 如图所示,在电梯中的斜面上放置了一滑块,在电梯加速上升的过程中,滑块相对斜面静止,则在该过程中( )
如图所示,在电梯中的斜面上放置了一滑块,在电梯加速上升的过程中,滑块相对斜面静止,则在该过程中( )
 如图所示,在电梯中的斜面上放置了一滑块,在电梯加速上升的过程中,滑块相对斜面静止,则在该过程中( )
如图所示,在电梯中的斜面上放置了一滑块,在电梯加速上升的过程中,滑块相对斜面静止,则在该过程中( )| A. | 斜面对滑块的弹力对滑块所做的功等于滑块增加的重力势能 | |
| B. | 滑块所受合力对滑块所做的功等于滑块增加的机械能 | |
| C. | 斜面对滑块的摩擦力对滑块做负功 | |
| D. | 斜面对滑块的弹力对滑块所做的功小于滑块增加的机械能 |

 如图为振动在细绳上传播所产生的波形在t=0,t=$\frac{T}{4}$和t=$\frac{T}{2}$时刻的波形图,试在图上画出t=$\frac{5T}{4}$时刻的波形图.
如图为振动在细绳上传播所产生的波形在t=0,t=$\frac{T}{4}$和t=$\frac{T}{2}$时刻的波形图,试在图上画出t=$\frac{5T}{4}$时刻的波形图.