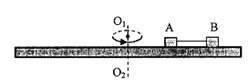
��Ŀ����
����Ŀ����ͼ��ʾΪ�ϡ����������L=10m����Ǧ�=37�㡢ʼ����v=5m/s������˳ʱ��ת���Ĵ��ʹ������ʹ�ʼ�ձ���������һ������ڴ��ʹ����϶��ɾ�ֹ�ͷŻ��£�����t=2s�����¶ˣ��������ٶ�gȡ10m/s2 �� sin37��=0.6��cos37��=0.8����
��1�����ʹ��������Ķ�Ħ���������
��2����������ʹ���ʱ��ת�����������ٶ��ʱ������Ӵ��ʹ��϶��ɾ�ֹ�ͷ������ص����¶ˣ�
���𰸡�
��1���⣺���ʹ�˳ʱ��ת����������ã�L= ![]() at2��
at2��
��ã�a= ![]() =5m/s2��
=5m/s2��
����ţ�ٵڶ����ɵã�mgsin������mgcos��=ma��
����=0.125��
�𣺴��ʹ��������Ķ�Ħ������Ϊ0.125��
��2���⣺������ʹ���ʱ��ת����Ҫʹ����Ӵ��ʹ��϶��ɾ�ֹ�ͷ������ص����¶ˣ�����Ҫ�������ش��ʹ����µ������ٶȣ�������Ħ�����ش��ʹ����£�
���ʱ���ʹ��ٶ�Ϊvm��������ٶ�Ϊa'��
��ţ�ٵڶ����ɵ� mgsin��+Ff=ma��
��Ff=��mgcos��
����λ���ٶȹ�ʽ�ã�vm2=2La'
��ã�vm= ![]() =11.8m/s��
=11.8m/s��
����������ʹ���ʱ��ת������������11.8m/sʱ������Ӵ��ʹ��϶��ɾ�ֹ�ͷ������ص����¶ˣ�
����������1�����ʹ�˳ʱ��ת��������»�ʱ�ܵ������ϵĻ���Ħ�����������˶�ѧ������ʽ��ţ�ٵڶ�������ʽ������Ħ����������2��������ʹ���ʱ��ת����Ҫʹ����Ӵ� �ʹ��϶��ɾ�ֹ�ͷ������ص����¶ˣ����� Ҫ�������ش��ʹ����µ������ٶȼ�����Ħ�����ش��ʹ����£�����ţ�ٵڶ�������������ٶȣ��ٸ����ȼ����˶�λ���ٶȹ�ʽ��⣮
�����㾫����������Ĺؼ��������⻬��Ħ���������֪ʶ�����ջ���Ħ����:���ù�ʽf=��F N ���м��㣬����FN ���������ѹ������һ������������������������ܺ�������.���߸���������˶�״̬������ƽ��������ţ�ٶ�������⣬�Լ����ȱ���ֱ���˶����ٶȡ�λ�ơ�ʱ��Ĺ�ϵ�����⣬�˽��ٶȹ�ʽ��V=V0+at��λ�ƹ�ʽ��s=v0t+1/2at2���ٶ�λ�ƹ�ʽ��vt2-v02=2as�����ϸ�ʽ��Ϊʸ��ʽ��Ӧ��ʱӦ�涨������Ȼ���ʸ����Ϊ��������⣬ͨ��ѡ���ٶȷ���Ϊ�������Ǹ�������һ�µ�ȡ��+��ֵ�����������෴��ȡ��-��ֵ��