题目内容
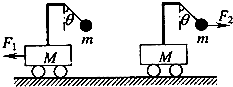 如图所示,两个完全相同的小车质量为M,放在光滑的水平面上,小车横梁上用细线各悬挂一质量为m(m<M)的小球,若分别施加水平恒力F1、F2,整个装置分别以加速度a1、a2做匀加速运动,但两条细线与竖直方向夹角均为θ,则下列判断正确的是( )
如图所示,两个完全相同的小车质量为M,放在光滑的水平面上,小车横梁上用细线各悬挂一质量为m(m<M)的小球,若分别施加水平恒力F1、F2,整个装置分别以加速度a1、a2做匀加速运动,但两条细线与竖直方向夹角均为θ,则下列判断正确的是( )分析:运用整体法和隔离法,对小球和整体进行分析,求出绳子的拉力、加速度,比较出拉力的大小和加速度大小.再对整体分析,根据牛顿第二定律比较出水平恒力的大小,以及在竖直方向上合力等于零,比较出支持力的大小.
解答:解:先对右图中情况下的整体受力分析,受重力、支持力和拉力
根据牛顿第二定律,有
F2=(M+m)a ①
再对左图中情况下的小球受力分析,如图
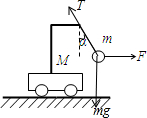
根据牛顿第二定律,有
F2-T2sinα=ma2 ②
T2cosα-mg=0 ③
由以上三式可解得
T2=
,a2=
.
再对左图中小球受力分析,如图
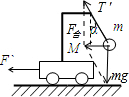
由几何关系得
F合=mgtanα T1=
则a1=
=gtanα
因为m<M,则a1>a2.拉力T1=T2.
对整体分析,F合=(M+m)a,则F1>F2.
在竖直方向上有:N=(M+m)g,所以N1=N2.故B正确,A、C、D错误.
故选B.
根据牛顿第二定律,有
F2=(M+m)a ①
再对左图中情况下的小球受力分析,如图

根据牛顿第二定律,有
F2-T2sinα=ma2 ②
T2cosα-mg=0 ③
由以上三式可解得
T2=
| mg |
| cosα |
| mgtanα |
| M |
再对左图中小球受力分析,如图

由几何关系得
F合=mgtanα T1=
| mg |
| cosα |
则a1=
| mgtanα |
| m |
因为m<M,则a1>a2.拉力T1=T2.
对整体分析,F合=(M+m)a,则F1>F2.
在竖直方向上有:N=(M+m)g,所以N1=N2.故B正确,A、C、D错误.
故选B.
点评:本题关键要多次对小球和整体受力分析,求出合力,得出加速度和绳子拉力进行比较.

练习册系列答案
相关题目
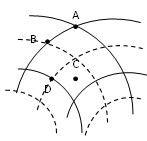
 (2012?金山区一模)如图所示,两个完全相同的波源在介质中形成的波相叠加而发生的干涉的示意图,实线表示波峰,虚线表示波谷,则( )
(2012?金山区一模)如图所示,两个完全相同的波源在介质中形成的波相叠加而发生的干涉的示意图,实线表示波峰,虚线表示波谷,则( ) (2008?上海模拟)如图所示,两个完全相同的波源在介质中形成的波相叠加而发生的干涉的示意图,实线表示波峰,虚线表示波谷,则( )
(2008?上海模拟)如图所示,两个完全相同的波源在介质中形成的波相叠加而发生的干涉的示意图,实线表示波峰,虚线表示波谷,则( )