题目内容
 一列横波沿x轴传播,速度为12m/s,在x轴上有A、B两点,它们各自的坐标分别为xA=7cm,xB=10cm,当A点在正的最大位移处时,B点恰在平衡位置且振动方向向下,如图所示,求这列波的频率的表达式和各表达式中的最小频率及与之对应的波长.
一列横波沿x轴传播,速度为12m/s,在x轴上有A、B两点,它们各自的坐标分别为xA=7cm,xB=10cm,当A点在正的最大位移处时,B点恰在平衡位置且振动方向向下,如图所示,求这列波的频率的表达式和各表达式中的最小频率及与之对应的波长.分析:根据A、B两点的状态关系,结合波形确定它们之间的距离与波长的关系,得到波长的通项,再求出频率的通项,求出最小频率和波长.分沿x轴正方向和x轴负方向传播两个方向进行研究.
解答:解:(1)若波沿x轴正方向传播,由题意得到
xB-xA=(n+
)λ
得到波长λ=
(n=0,1,2,3…)
则频率f=
=
=100(4n+3)Hz (n=0,1,2,3…)
最小频率n=0,fmin=
=300Hz,
最小波长n=0,λmin=
=4×10-2m.
(2)若波沿x轴负方向传播,则f=
=
=100(4n+1)Hz (n=0,1,2,3…)
最小频率n=0,fmin=
=100Hz
最小波长n=0,λmin=
=12×10-2m
答:若波沿x轴正方向传播,频率f=100(4n+3)Hz (n=0,1,2,3…),最小频率为300Hz,
最小波长为4×10-2m.若波沿x轴负方向传播,则f=100(4n+1)Hz (n=0,1,2,3…),最小频率为100Hz
最小波长为12×10-2m.
xB-xA=(n+
| 3 |
| 4 |
得到波长λ=
| xB-xA | ||
n+
|
则频率f=
| v |
| λ |
v(n+
| ||
| xB-xA |
最小频率n=0,fmin=
12×
| ||
| 3×10-2 |
最小波长n=0,λmin=
| 3×10-2 | ||
|
(2)若波沿x轴负方向传播,则f=
| v |
| λ |
v(n+
| ||
| xB-xA |
最小频率n=0,fmin=
12×
| ||
| 3×10-2 |
最小波长n=0,λmin=
| 3×10-2 | ||
|
答:若波沿x轴正方向传播,频率f=100(4n+3)Hz (n=0,1,2,3…),最小频率为300Hz,
最小波长为4×10-2m.若波沿x轴负方向传播,则f=100(4n+1)Hz (n=0,1,2,3…),最小频率为100Hz
最小波长为12×10-2m.
点评:知道两个质点在同一时刻的状态,要结合波形分析距离与波长的关系,考查运用数学知识列通项的能力.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
 如图所示,一列横波沿x轴传播,实线和虚线分别是t1时刻和t2时刻的图象其中t2=t1+
如图所示,一列横波沿x轴传播,实线和虚线分别是t1时刻和t2时刻的图象其中t2=t1+ 如图所示,已知一列横波沿x轴传播,实线和虚线分别是t1时刻和t2时刻的图象.已知
如图所示,已知一列横波沿x轴传播,实线和虚线分别是t1时刻和t2时刻的图象.已知 如图所示,一列横波沿x轴传播,t0时刻波的图象如图中实线所示;经△t=0.2s,波的图象如图中虚线所示.已知其波长为2m,则下述说法中正确的是( )
如图所示,一列横波沿x轴传播,t0时刻波的图象如图中实线所示;经△t=0.2s,波的图象如图中虚线所示.已知其波长为2m,则下述说法中正确的是( )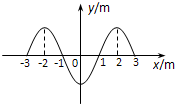 一列横波沿x轴传播,传播方向未知.t时刻与t+0.4s时刻波形相同,两时刻在x轴上-3m~3m的区间内的波形如图所示.由图象可以判定
一列横波沿x轴传播,传播方向未知.t时刻与t+0.4s时刻波形相同,两时刻在x轴上-3m~3m的区间内的波形如图所示.由图象可以判定