题目内容
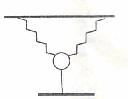
 如图,两根完全相同的轻弹簧下挂一个质量为,m的小球,小球与地面间有一竖直细线相连,系统平衡.已知两弹簧之间的夹角是120°,且弹簧产生的弹力均为3mg,则剪断细线的瞬间,小球的加速度是( )
如图,两根完全相同的轻弹簧下挂一个质量为,m的小球,小球与地面间有一竖直细线相连,系统平衡.已知两弹簧之间的夹角是120°,且弹簧产生的弹力均为3mg,则剪断细线的瞬间,小球的加速度是( )分析:分析剪断细线前,由平衡条件求解绳子的拉力,剪断细线瞬间,弹簧的弹力没有变化,小球的合力与剪断细线前细线的拉力大小相等,方向相反,根据牛顿第二定律求解剪断细线的瞬间小球的加速度.
解答:解:剪断细线前,小球受到重力mg、两弹簧的拉力,各是3mg,及细线的拉力F,由于两弹簧之间的夹角是120,则两弹力的合力大小等于3mg,方向竖直向上,由平衡条件得知,细线的拉力大小等于F=3mg-mg=2mg,方向竖直向下.
剪断细线瞬间,弹簧的弹力没有变化,小球的合力与剪断细线前细线的拉力大小相等,方向相反,即此瞬间小球的合力大小为F合=2mg,方向竖直向上,根据牛顿第二定律得知,小球的加速度为a=
=2g,方向竖直向上.
故选C
剪断细线瞬间,弹簧的弹力没有变化,小球的合力与剪断细线前细线的拉力大小相等,方向相反,即此瞬间小球的合力大小为F合=2mg,方向竖直向上,根据牛顿第二定律得知,小球的加速度为a=
| F合 |
| m |
故选C
点评:本题是瞬时问题,往往先研究剪断细线前小球的受力情况,抓住剪断细线瞬间弹力不变,根据牛顿第二定律研究加速度.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目