题目内容
 (2013?静安区二模)有人设计了一种测定液体温度的仪器,其结构如图所示.在两端封闭、粗细均匀的竖直玻璃管内,有一段长10cm的水银柱将管内气体分隔成上、下两部分,上部分气柱长20cm、压强为50cmHg,下部分气柱长5cm.今将玻璃管下部插入待测液体中(上部分气体温度始终与环境温度相同,上下两部分气体可以认为没有热交换),这时水银柱向上移动了2cm,已知环境温度是20°C,试问:
(2013?静安区二模)有人设计了一种测定液体温度的仪器,其结构如图所示.在两端封闭、粗细均匀的竖直玻璃管内,有一段长10cm的水银柱将管内气体分隔成上、下两部分,上部分气柱长20cm、压强为50cmHg,下部分气柱长5cm.今将玻璃管下部插入待测液体中(上部分气体温度始终与环境温度相同,上下两部分气体可以认为没有热交换),这时水银柱向上移动了2cm,已知环境温度是20°C,试问:(1)此时上部分气体的压强为多少cmHg?
(2)待测液体的温度是多少°C?(计算结果保留一位小数)
分析:(1)上部分气体发生等温变化,由玻意耳定律求出此时上部分气体的压强;
(2)下部分气体P、V、T三个参量都变化,根据理想气体状态求解温度,抓住下部分气体的压强等于上部分气体的压强与水银柱压强之和.
(2)下部分气体P、V、T三个参量都变化,根据理想气体状态求解温度,抓住下部分气体的压强等于上部分气体的压强与水银柱压强之和.
解答:解:(1)上部分气体作等温变化,由玻意耳定律得,p1V1=p1′V1′
即p1l1S=p1′l1′S,
得 p1′=
=
cmHg≈55.6cmHg
(2)下部气体作一般变化
插入前,下部分气体压强p2=p1+ρgh=50+10=60 cmHg,气柱长度l2=5cm,温度t1=20℃
插入后,下部分气体压强p2′=p1′+ρgh=(55.6+10)cmHg=65.6 cmHg,气柱长度l2′=7cm,温度t2=?
由理想气体状态方程得:
=
代入解得,t2=175.5℃
答:(1)此时上部分气体的压强为55.6cmHg.
(2)待测液体的温度是175.5℃.
即p1l1S=p1′l1′S,
得 p1′=
| P1l1 |
| l1′ |
| 50×20 |
| 18 |
(2)下部气体作一般变化
插入前,下部分气体压强p2=p1+ρgh=50+10=60 cmHg,气柱长度l2=5cm,温度t1=20℃
插入后,下部分气体压强p2′=p1′+ρgh=(55.6+10)cmHg=65.6 cmHg,气柱长度l2′=7cm,温度t2=?
由理想气体状态方程得:
| P2l2S |
| 273+t1 |
| P2′l2′S |
| 273+t2 |
代入解得,t2=175.5℃
答:(1)此时上部分气体的压强为55.6cmHg.
(2)待测液体的温度是175.5℃.
点评:本题能用静力学观点找出两部分压强的关系,是解题的关键.要注意研究过程中哪些量不变,哪些量变化.能够用物理规律把所要研究的物理量表示出来.

练习册系列答案
相关题目
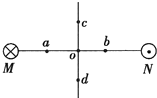 (2013?静安区二模)如图,两根互相平行的长直导线过纸面上的M、N两点,且与纸面垂直,导线中通有大小相等、方向相反的电流.a、o、b在M、N的连线上,o为MN的中点,c、d位于MN的中垂线上,且a、b、c、d到o点的距离均相等.关于以上几点处的磁场,下列说法正确的是( )
(2013?静安区二模)如图,两根互相平行的长直导线过纸面上的M、N两点,且与纸面垂直,导线中通有大小相等、方向相反的电流.a、o、b在M、N的连线上,o为MN的中点,c、d位于MN的中垂线上,且a、b、c、d到o点的距离均相等.关于以上几点处的磁场,下列说法正确的是( )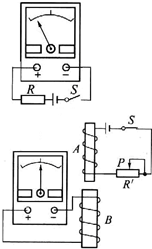 (2013?静安区二模)在“研究电磁感应现象”的实验中,首先按右上图接线,以查明电流表指针的偏转方向与电流方向之间的关系.当闭合S时观察到电流表指针向左偏,不通电时电流表指针停在正中央.然后按如图所示将电流表与线圈B连成一个闭合回路,将线圈A、电池、滑动变阻器和电键S串联成另一个闭合电路.
(2013?静安区二模)在“研究电磁感应现象”的实验中,首先按右上图接线,以查明电流表指针的偏转方向与电流方向之间的关系.当闭合S时观察到电流表指针向左偏,不通电时电流表指针停在正中央.然后按如图所示将电流表与线圈B连成一个闭合回路,将线圈A、电池、滑动变阻器和电键S串联成另一个闭合电路.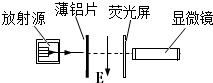 (2013?静安区二模)如图所示为研究某未知元素放射性的实验装置,实验开始时在薄铝片和荧光屏之间有图示方向的匀强电场E,通过显微镜可以观察到,在荧光屏的某一位置上每分钟闪烁的亮点数.若撤去电场后继续观察,发现每分钟闪烁的亮点数没有变化;如果再将薄铝片移开,观察到每分钟闪烁的亮点数大大增加,由此可以判断,放射源发出的射线可能为( )
(2013?静安区二模)如图所示为研究某未知元素放射性的实验装置,实验开始时在薄铝片和荧光屏之间有图示方向的匀强电场E,通过显微镜可以观察到,在荧光屏的某一位置上每分钟闪烁的亮点数.若撤去电场后继续观察,发现每分钟闪烁的亮点数没有变化;如果再将薄铝片移开,观察到每分钟闪烁的亮点数大大增加,由此可以判断,放射源发出的射线可能为( )