Question

【题目】一弹簧一端固定在倾角为37°光滑斜面的底端，另一端拴住的质量m1=4kg的物块P，Q为一重物，已知Q的质量m2=8kg，弹簧的质量不计，劲度系数k=600N/m，系统处于静止，如右图所示．现给Q施加一个方向沿斜面向上的力F，使它从静止开始斜向上做匀加速运动，已知在前0.2s时间内，F为变力，0.2s以后，F为恒力．求力F的最大值与最小值．（g=10m/s2）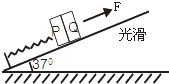

Answer 1

【答案】解：设刚开始时弹簧压缩量为x0

则（m1+m2）gsin θ=kx0①

因为在前0.2 s时间内，F为变力，0.2 s以后，F为恒力，所以在0.2 s时，P对Q的作用力为0，

由牛顿第二定律知

kx1﹣m1gsin θ=m1a ②

前0.2 s时间内P、Q向上运动的距离为

x0﹣x1= at2③

①②③式联立解得a=3 m/s2

当P、Q开始运动时拉力最小，此时有

Fmin=（m1+m2）a=36 N

当P、Q分离时拉力最大，此时有

Fmax=m2（a+gsin θ）=72 N．

答：最大值72N，最小值36N

【解析】先根据平衡条件求出弹簧开始的压缩量，因为在前0.2 s时间内，F为变力，0.2s以后，F为恒力，所以在0.2s时，P对Q的作用力为0，由牛顿第二定律求出匀加速运动的加速度，当P、Q开始运动时拉力最小，当P、Q分离时拉力最大，根据牛顿第二定律即可求解．