题目内容
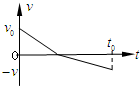 某同学在地面上将质量为m的一物块以初速度V0竖直向上抛出,经过t0时间,物块以速率落回该同学手中.物块运动的ν-t图如图,求
某同学在地面上将质量为m的一物块以初速度V0竖直向上抛出,经过t0时间,物块以速率落回该同学手中.物块运动的ν-t图如图,求(1)物块上升的最大高度;
(2)物块运动过程中所受空气阻力大小.
分析:v-t图象与时间轴围成图形的面积等于位移大小;
根据牛顿第二定律列方程即可求解.
根据牛顿第二定律列方程即可求解.
解答:解:(1)设上升时间t1,下落时间t2,则上升最大高度h=
t1=
t2
又t1+t2=t0
得t1=
t0 t2=
t0
则:h=
?t0
(2)上升过程,根据运动学公式:a1=-
=-
又由牛顿第二定律:-(f+mg)=ma1
得:f=m[
-g]
答:(1)物块上升的最大高度
;
(2)物块运动过程中所受空气阻力大小
-mg.
| v0 |
| 2 |
| v |
| 2 |
又t1+t2=t0
得t1=
| v |
| v0+v |
| v0 |
| v0+v |
则:h=
| 1 |
| 2 |
| v0v |
| v0+v |
(2)上升过程,根据运动学公式:a1=-
| v0 |
| t1 |
| v0(v0+v) |
| vt0 |
又由牛顿第二定律:-(f+mg)=ma1
得:f=m[
| v0(v0+v) |
| vt0 |
答:(1)物块上升的最大高度
| 1 |
| 2 |
| v0vt0 |
| v0+v |
(2)物块运动过程中所受空气阻力大小
| mv0(v0+v) |
| vt0 |
点评:本题考查了v-t图象以及牛顿第二定律的应用,牛顿第二定律是运动与力结合的桥梁.

练习册系列答案
相关题目
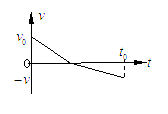 某同学在地面上将质量为m的一物块以初速度V
某同学在地面上将质量为m的一物块以初速度V