��Ŀ����
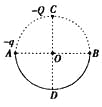
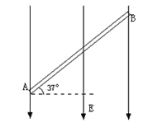
����Ŀ����ͼ��ʾ��һ����Ϊ2 m�ľ�Եϸ��AB��������ǿ�糡E�У���A��B�������ô��ڵ糡�����ұ߽��ϣ������=37��,�糡ǿ��E=103 V/m��������ֱ���£�������һ���������С����G=10-3 N,�����q=2��10-6 C����A���ɾ�ֹ��ʼ�˶�����֪С����ܱڵĶ�Ħ������Ϊ0��5����С���B�����ʱ���ٶ��Ƕ��٣���ȡg=10 m/s2��sin37��=0��6��cos37��=0��8��
���𰸡�2![]() m/s��
m/s��
��������
�����������С��Ϊ�о����������������������ͼ����ͼ������ƽ�������õ���
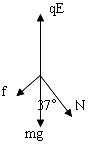
���Ӷ�С���ѹ��N=��qE-mg��cos37��=��2��10-6��103-10-4��10����0��8N=8��10-4N
С���˶����������ܵ�Ħ�����Ĵ�Сf=��N=0��5��8��10-4N=4��10-4N
С���A��B�Ĺ����У����ݶ��ܶ�������F-mg��Lsin37��-fL=![]() mv2
mv2
�����ã�С���B�����ʱ���ٶ�v=2![]() m/s��
m/s��

��ϰ��ϵ�д�
 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
�����Ŀ