题目内容
【题目】如图所示,PM是半径为R的光滑四分之一绝缘轨道,在该轨道内有垂直纸面向外的匀强次大红,磁感应强度大小为B。MN水平且足够长,PM下端与MN相切于M点。质量为m的带正电小球b静止在水平轨道上,质量为2m、电荷量为q的带正电小球a从P点静止释放,在a球进入水平轨道后,a、b两小球间只有静电力作用,且a、b两小球始终没有接触。带电小球均可视为点电荷,设小球b离M点足够远,重力加速度为g。求:
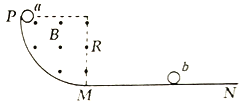
(1)小球a刚到达M点时速度大小及对轨道的压力大小;
(2)a、b两小球系统的电势能最大值EP;
(3)a、b两小球最终的速度va、vb的大小。
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
![]()
【解析】试题分析:(1)从P到M,洛伦兹力、弹力不做功,只有重力做功,由动能定理即可求小球到达M点的速度,根据牛顿第二定律可求出轨道对小球的支持力,根据牛顿第三定律可求出小球对轨道的压力大小;(2)进入水平轨道,a、b两小球间只有静电力作用,当两者速度相等时两个小球系统的电势能最大值;(3)由动量守恒定律和能量守恒定律可求出两小球的最终速度大小.
(1)从P到M,洛伦兹力、弹力不做功,只有重力做功
由动能定理有: ![]()
解得: ![]()
由牛顿第二定律有: ![]()
解得: ![]()
根据牛顿第三定律得小球对轨道的压力为: ![]()
(2)两球速度相等时系统电势能最大,由动量守恒定律有: ![]()
根据能量转化与守恒定律有: ![]()
解得: ![]()
(3)由动量守恒定律: ![]()
由能量转化与守恒定律有: ![]()
解得: ![]() ,
, ![]()

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目