题目内容
19. 如图所示,有一平行纸面的直角坐标系xOy,坐标轴Oy垂直于水平金属板,在其POy区域内有垂直纸面向外,磁感应强度为B的匀强磁场,磁场边界OP与x轴正方向夹角为30°;POx区域为无场区.一质量为m,带电荷量为+q的粒子沿从A(0,b)点垂直于y轴进入第Ⅰ象限POy区域,经OP上某点离开磁场,最后沿与x轴正向成60°角的方向离开第Ⅰ象限,不计粒子重力,求:粒子进入磁场的初速度大小.
如图所示,有一平行纸面的直角坐标系xOy,坐标轴Oy垂直于水平金属板,在其POy区域内有垂直纸面向外,磁感应强度为B的匀强磁场,磁场边界OP与x轴正方向夹角为30°;POx区域为无场区.一质量为m,带电荷量为+q的粒子沿从A(0,b)点垂直于y轴进入第Ⅰ象限POy区域,经OP上某点离开磁场,最后沿与x轴正向成60°角的方向离开第Ⅰ象限,不计粒子重力,求:粒子进入磁场的初速度大小.
分析 粒子在磁场中华做匀速直线运动,洛伦兹力提供向心力,作出粒子运动轨迹,求出粒子轨道半径,应用牛顿第二定律求出粒子的速度.
解答 解:粒子在磁场中做匀速圆周运动,粒子运动轨迹如图所示:
沿与x轴正向成60°角的方向离开第Ⅰ象限,OP与x轴正方向成30°角,
则粒子离开磁场时的速度与OP垂直,O点是粒子做圆周运动的圆心,
由几何知识可知,粒子做圆周运动的轨道半径:R=OA=b,
粒子做圆周运动,洛伦兹力提供向心力,由牛顿第二定律得:
qvB=m$\frac{{v}^{2}}{R}$,解得,粒子的速度:v=$\frac{qBb}{m}$;
答:粒子进入磁场的初速度大小为$\frac{qBb}{m}$.
点评 本题考查了粒子在磁场中的运动,分析清楚粒子运动过程,应用牛顿第二定律可以解题,作出粒子运动轨迹,根据几何知识求出粒子的轨道半径是正确解题的关键.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案
相关题目
8. 如图所示,一列简谐波向右以8.0m/s的速度传播,某一时刻沿波的传播方向上有a、b两质点,位移大小相等,方向相同,则( )
如图所示,一列简谐波向右以8.0m/s的速度传播,某一时刻沿波的传播方向上有a、b两质点,位移大小相等,方向相同,则( )
 如图所示,一列简谐波向右以8.0m/s的速度传播,某一时刻沿波的传播方向上有a、b两质点,位移大小相等,方向相同,则( )
如图所示,一列简谐波向右以8.0m/s的速度传播,某一时刻沿波的传播方向上有a、b两质点,位移大小相等,方向相同,则( )| A. | 无论再经多长时间,a、b两质点位移不可能大小相等、方向相反 | |
| B. | 再经过0.25s,a、b两质点位移第一次大小相等、方向相反 | |
| C. | 再经过0.25s,a、b两质点速度第一次大小相等、方向相反 | |
| D. | 再经过0.5s,a、b两质点速度第一次大小相等、方向相同 |
4.一人造地球卫星绕地球做匀速圆周运动,假如该卫星变轨后仍做匀速圆周运动,速度减小为原来的$\frac{1}{2}$,不考虑卫星质量的变化,则变轨前后卫星的( )
| A. | 角速度之比为2:1 | B. | 向心加速度之比为4:1 | ||
| C. | 周期之比为1:8 | D. | 向心力之比为16:1 |
11. 物体A、B、C均静止在同一水平面上,它们的质量分别为mA、mB、mC,与水平面的动摩擦因素分别为μA、μB、μC,用平行于水平面的拉力F分别拉物体A、B、C,所得加速度a 与拉力F的关系图线如图所对应的直线甲、乙、丙所示,甲、乙两直线平行,则以下说法正确的是( )
物体A、B、C均静止在同一水平面上,它们的质量分别为mA、mB、mC,与水平面的动摩擦因素分别为μA、μB、μC,用平行于水平面的拉力F分别拉物体A、B、C,所得加速度a 与拉力F的关系图线如图所对应的直线甲、乙、丙所示,甲、乙两直线平行,则以下说法正确的是( )
 物体A、B、C均静止在同一水平面上,它们的质量分别为mA、mB、mC,与水平面的动摩擦因素分别为μA、μB、μC,用平行于水平面的拉力F分别拉物体A、B、C,所得加速度a 与拉力F的关系图线如图所对应的直线甲、乙、丙所示,甲、乙两直线平行,则以下说法正确的是( )
物体A、B、C均静止在同一水平面上,它们的质量分别为mA、mB、mC,与水平面的动摩擦因素分别为μA、μB、μC,用平行于水平面的拉力F分别拉物体A、B、C,所得加速度a 与拉力F的关系图线如图所对应的直线甲、乙、丙所示,甲、乙两直线平行,则以下说法正确的是( )| A. | μA<μB mA=mB | B. | μB>μC mB>m C | C. | μB=μC mB>mC | D. | μA<μC mA>mC |
8. 如图所示,在水平向右的匀强电场中有一绝缘斜面,斜面上有一带电金属块沿斜面滑下,已知在金属块滑下的过程中动能增加了12J,金属块克服摩擦力做功8J,重力做功24J,则以下判断正确的是( )
如图所示,在水平向右的匀强电场中有一绝缘斜面,斜面上有一带电金属块沿斜面滑下,已知在金属块滑下的过程中动能增加了12J,金属块克服摩擦力做功8J,重力做功24J,则以下判断正确的是( )
 如图所示,在水平向右的匀强电场中有一绝缘斜面,斜面上有一带电金属块沿斜面滑下,已知在金属块滑下的过程中动能增加了12J,金属块克服摩擦力做功8J,重力做功24J,则以下判断正确的是( )
如图所示,在水平向右的匀强电场中有一绝缘斜面,斜面上有一带电金属块沿斜面滑下,已知在金属块滑下的过程中动能增加了12J,金属块克服摩擦力做功8J,重力做功24J,则以下判断正确的是( )| A. | 金属块带负电荷 | |
| B. | 电场力做功4 J | |
| C. | 金属块的电势能与动能之和增加了16 J | |
| D. | 金属块的机械能减少12 J |
9. 如图所示,螺线管B套在螺线管A外边,螺线管A经过滑动变阻器和开关S2与电源相连接构成直流闭合电路;螺线管B与开关S1、灵敏电流计构成另一闭合回路.进行下列操作,没有产生电磁感应现象的是( )
如图所示,螺线管B套在螺线管A外边,螺线管A经过滑动变阻器和开关S2与电源相连接构成直流闭合电路;螺线管B与开关S1、灵敏电流计构成另一闭合回路.进行下列操作,没有产生电磁感应现象的是( )
 如图所示,螺线管B套在螺线管A外边,螺线管A经过滑动变阻器和开关S2与电源相连接构成直流闭合电路;螺线管B与开关S1、灵敏电流计构成另一闭合回路.进行下列操作,没有产生电磁感应现象的是( )
如图所示,螺线管B套在螺线管A外边,螺线管A经过滑动变阻器和开关S2与电源相连接构成直流闭合电路;螺线管B与开关S1、灵敏电流计构成另一闭合回路.进行下列操作,没有产生电磁感应现象的是( )| A. | 闭合S1,接通S2的瞬间 | |
| B. | 闭合S1和S2,断开S2的瞬间 | |
| C. | 闭合S1和S2,断开S1的瞬间 | |
| D. | 断开S1,闭合S2,滑动滑动变阻器滑片的过程中 |
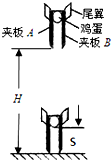 某学校的一个实验研究小组,以“保护鸡蛋”为题,要求制作一个装置,让鸡蛋从高处落到地面而不被摔坏.鸡蛋要不被摔坏,直接撞击地面的最大速度不能超过3.0m/s.现有一位同学设计了如图所示的一个装置:用A、B两块较粗糙的夹板夹住鸡蛋,鸡蛋夹放的位置离装置下端的距离s=0.4m,当鸡蛋相对夹板运动时,A、B夹板与鸡蛋之间的总摩擦力为鸡蛋重力的8倍,现将该装置从距地面某一高处自由落下,装置碰地后速度为0,且保持竖直不反弹.运动过程不计空气阻力,不计装置与地面作用时间.g=10m/s2
某学校的一个实验研究小组,以“保护鸡蛋”为题,要求制作一个装置,让鸡蛋从高处落到地面而不被摔坏.鸡蛋要不被摔坏,直接撞击地面的最大速度不能超过3.0m/s.现有一位同学设计了如图所示的一个装置:用A、B两块较粗糙的夹板夹住鸡蛋,鸡蛋夹放的位置离装置下端的距离s=0.4m,当鸡蛋相对夹板运动时,A、B夹板与鸡蛋之间的总摩擦力为鸡蛋重力的8倍,现将该装置从距地面某一高处自由落下,装置碰地后速度为0,且保持竖直不反弹.运动过程不计空气阻力,不计装置与地面作用时间.g=10m/s2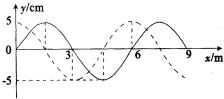 一列横波沿x轴传播,t1时刻的波形如图中实线所示,t2时刻的波形如图中虚线所示.已知t2=(t1+1$\frac{3}{8}$)s,振源振动周期为0.5s,则波的传播方向是沿x轴正方向,从t1时刻到t2时刻波传播距离是16.5m.
一列横波沿x轴传播,t1时刻的波形如图中实线所示,t2时刻的波形如图中虚线所示.已知t2=(t1+1$\frac{3}{8}$)s,振源振动周期为0.5s,则波的传播方向是沿x轴正方向,从t1时刻到t2时刻波传播距离是16.5m. 如图所示,一根细绳一端系于水平地面上,另一端系于竖直墙壁上,在绳上O点处竖直向上加一个拉力大小为F,OA与水平面夹角为θ,绳OB垂直于墙壁,此时处于平衡状态.
如图所示,一根细绳一端系于水平地面上,另一端系于竖直墙壁上,在绳上O点处竖直向上加一个拉力大小为F,OA与水平面夹角为θ,绳OB垂直于墙壁,此时处于平衡状态.