题目内容
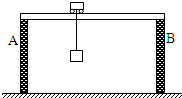
 如图所示为龙门吊车的示意图,质量为2t的均匀水平横梁,架在相距8m的A、B两面竖直墙上,一质量为3.2t的吊车停在横梁上距A墙3m处.不计墙的厚度和吊车的大小,则当吊车下端未悬吊重物时,A墙承受的压力等于________ N;若吊车将一质量为1.6t的重物P向上吊起,P到横梁的距离以d=H-2.5t2(SI)(SI表示国际单位制,式中H为横梁离地面的高度)规律变化时,A墙承受的压力等于________N.(g取10m/s2)
如图所示为龙门吊车的示意图,质量为2t的均匀水平横梁,架在相距8m的A、B两面竖直墙上,一质量为3.2t的吊车停在横梁上距A墙3m处.不计墙的厚度和吊车的大小,则当吊车下端未悬吊重物时,A墙承受的压力等于________ N;若吊车将一质量为1.6t的重物P向上吊起,P到横梁的距离以d=H-2.5t2(SI)(SI表示国际单位制,式中H为横梁离地面的高度)规律变化时,A墙承受的压力等于________N.(g取10m/s2)
3×104 4.5×104
分析:1、以B点为支点,根据力矩平衡FA?L=m车g? L+m梁g?
L+m梁g? L,代入数据,可以解得A墙对梁的作用力FA,再根据牛顿第三定律,可得A墙受到的承受力等于FA.
L,代入数据,可以解得A墙对梁的作用力FA,再根据牛顿第三定律,可得A墙受到的承受力等于FA.
2、当吊车将一质量为1.6t的重物P向上吊起,P到横梁的距离以d=H-2.5t2规律变化时,根据运动学公式得到加速度;对重物,根据牛顿第二定律F-mg=ma,可解得车对重物的作用力F,根据牛顿第三定律,重物对车的作用力大小也为F.
故车对梁的作用力为F车=m车g+F.
仍以B点为支点,根据力矩平衡FA′?L=F车? L+m梁g?
L+m梁g? L
L
解答:以B点为支点,根据力矩平衡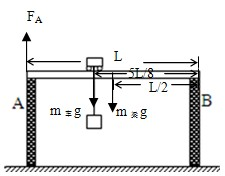
FA?L=m车g? L+m梁g?
L+m梁g? L
L
代入数据,FA×8=3.2×103×10×5+2×103×10×4
解得FA=3×104N.
根据牛顿第三定律,A墙受到的承受力为3×104N
2、当吊车将一质量为1.6t的重物P向上吊起,P到横梁的距离以d=H-2.5t2规律变化时,根据运动学公式x=v0t+ 得到加速度为5.0m/s2;
得到加速度为5.0m/s2;
对重物,根据牛顿第二定律F-mg=ma
所以车对重物的作用力F=mg+ma=1.6×103×(10+5)N=2.4×104N
根据牛顿第三定律,重物对车的作用力也为2.4×104N
故车对梁的作用力为F车=m车g+F=3.2×103×10+2.4×104=5.6×104N
仍以B点为支点,根据力矩平衡
FA′?L=F车? L+m梁g?
L+m梁g? L
L
代入数据,FA′×8=5.6×104×5+2×104×4
解得FA′=4.5×104N.
根据牛顿第三定律,A墙受到的承受力为4.5×104N
故答案为:3×104N、4.5×104N.
点评:本题是一道力矩平衡的问题,同时又综合了牛顿第二定律和牛顿第三定律,综合能力要求较高,是一道好题,属于中档题.
分析:1、以B点为支点,根据力矩平衡FA?L=m车g?
 L+m梁g?
L+m梁g? L,代入数据,可以解得A墙对梁的作用力FA,再根据牛顿第三定律,可得A墙受到的承受力等于FA.
L,代入数据,可以解得A墙对梁的作用力FA,再根据牛顿第三定律,可得A墙受到的承受力等于FA.2、当吊车将一质量为1.6t的重物P向上吊起,P到横梁的距离以d=H-2.5t2规律变化时,根据运动学公式得到加速度;对重物,根据牛顿第二定律F-mg=ma,可解得车对重物的作用力F,根据牛顿第三定律,重物对车的作用力大小也为F.
故车对梁的作用力为F车=m车g+F.
仍以B点为支点,根据力矩平衡FA′?L=F车?
 L+m梁g?
L+m梁g? L
L解答:以B点为支点,根据力矩平衡

FA?L=m车g?
 L+m梁g?
L+m梁g? L
L代入数据,FA×8=3.2×103×10×5+2×103×10×4
解得FA=3×104N.
根据牛顿第三定律,A墙受到的承受力为3×104N
2、当吊车将一质量为1.6t的重物P向上吊起,P到横梁的距离以d=H-2.5t2规律变化时,根据运动学公式x=v0t+
 得到加速度为5.0m/s2;
得到加速度为5.0m/s2;对重物,根据牛顿第二定律F-mg=ma
所以车对重物的作用力F=mg+ma=1.6×103×(10+5)N=2.4×104N
根据牛顿第三定律,重物对车的作用力也为2.4×104N
故车对梁的作用力为F车=m车g+F=3.2×103×10+2.4×104=5.6×104N
仍以B点为支点,根据力矩平衡
FA′?L=F车?
 L+m梁g?
L+m梁g? L
L代入数据,FA′×8=5.6×104×5+2×104×4
解得FA′=4.5×104N.
根据牛顿第三定律,A墙受到的承受力为4.5×104N
故答案为:3×104N、4.5×104N.
点评:本题是一道力矩平衡的问题,同时又综合了牛顿第二定律和牛顿第三定律,综合能力要求较高,是一道好题,属于中档题.

练习册系列答案
相关题目
 如图所示为龙门吊车的示意图,质量为2t的均匀横梁,架在相距8m的A、B两面墙上,一质量为3.2t的天车停在横梁上距A墙3m处.不计墙的厚度和天车大小的影响,当天车下端未悬吊重物时,A墙承受的压力是
如图所示为龙门吊车的示意图,质量为2t的均匀横梁,架在相距8m的A、B两面墙上,一质量为3.2t的天车停在横梁上距A墙3m处.不计墙的厚度和天车大小的影响,当天车下端未悬吊重物时,A墙承受的压力是 如图所示为龙门吊车的示意图,质量为2t的均匀横梁,架在相距8m的A、B两面墙上,一质量为3.2t的天车停在横梁上距A墙3m处.不计墙的厚度和天车大小的影响,求:
如图所示为龙门吊车的示意图,质量为2t的均匀横梁,架在相距8m的A、B两面墙上,一质量为3.2t的天车停在横梁上距A墙3m处.不计墙的厚度和天车大小的影响,求: (2009?虹口区一模)如图所示为龙门吊车的示意图,质量为2t的均匀水平横梁,架在相距8m的A、B两面竖直墙上,一质量为3.2t的吊车停在横梁上距A墙3m处.不计墙的厚度和吊车的大小,则当吊车下端未悬吊重物时,A墙承受的压力等于
(2009?虹口区一模)如图所示为龙门吊车的示意图,质量为2t的均匀水平横梁,架在相距8m的A、B两面竖直墙上,一质量为3.2t的吊车停在横梁上距A墙3m处.不计墙的厚度和吊车的大小,则当吊车下端未悬吊重物时,A墙承受的压力等于