题目内容
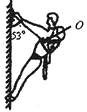
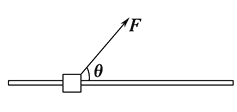
【题目】如图所示,将质量m=0.1 kg的圆环套在固定的水平直杆上.环的直径略大于杆的截面直径.环与杆间的动摩擦因数为μ=0.8.对环施加一位于竖直平面内斜向上且与杆夹角为θ=53°的拉力F,使圆环以a=4.4 m/s2的加速度沿杆运动,求F的大小.(取sin53°=0.8,cos53°=0.6,g=10 m/s2)
【答案】1 N或9 N
【解析】试题分析:根据平衡条件可求得恰好没有挤压时的拉力大小,再分别对上端挤压和下端挤压两种情况进行分析,根据牛顿第二定律列式即可求得F的大小。
当环与直杆之间没有作用力时,在垂直杆方向有Fsinθ=mg
代入数据解得:F=1.25 N
当F<1.25 N时,杆对环的弹力向上,对环进行受力分析,
根据牛顿第二定律有Fcosθ-μFN=ma,
根据平衡条件有:FN+Fsinθ=mg
联立解得:F=1 N
当F>1.25 N时,杆对环的弹力向下,对环进行受力分析,
根据牛顿第二定律有:F′cosθ-μF′N=ma,
根据平衡条件有:F′sinθ=mg+F′N
联立解得:F′=9 N.

练习册系列答案
相关题目