题目内容
4. 如图所示,R1=10Ω,R2=4Ω,R3=6Ω,R4=3Ω,AB间所加电压U=2.4V.若在C、D之间接一个伏特表,它的读数是1.8V;若在C、D之间接一个安培表,则它的读数是0.67A.
如图所示,R1=10Ω,R2=4Ω,R3=6Ω,R4=3Ω,AB间所加电压U=2.4V.若在C、D之间接一个伏特表,它的读数是1.8V;若在C、D之间接一个安培表,则它的读数是0.67A.
分析 (1)在ab间接一只理想电压表,R2、R3串联后与R1并联再与R4串联,电压表测量电阻R3、R4两端的电压之和.
(2)在ab间接一只理想电流表,此时R3、R4并联后,再与R1串联,这三个电阻组成串联电路后,再与电阻R2并联,电流表测量通过R2、R3的电流之和,根据欧姆定律和串、并联电阻的特点求出电流表的示数.
解答 解:若在C、D之间接一个伏特表,
R2、R3串联后电阻为R串=R2+R3=4Ω+6Ω=10Ω,R串与R1并联后电阻为R分=$\frac{{R}_{串}{R}_{1}}{{R}_{串}+{R}_{1}}$=5Ω,再与R4串联后总电阻为R总=R分+R4=5Ω+3Ω=8Ω,
此时电路电流I总=$\frac{U}{{R}_{总}}=\frac{2.4}{8}$=0.3A
R4两端的电压U4=I总R4=0.3A×3Ω=0.9V,
所以R2、R3串联后两端的电压为U串=U-U4=2.4V-0.9V=1.5V,
R2、R3串联后电流I分=$\frac{{U}_{串}}{{R}_{2}+{R}_{3}}=\frac{1.5}{4+6}$=0.15A,
R3两端的电压为U3=I分R3=0.15A×6Ω=0.9V,
电阻R3、R4两端的电压之和也就是电压表的示数U分=U3+U4=0.9V+0.9V=1.8V.
若在C、D之间接一个安培表,
通过电阻R2的电流I2=$\frac{U}{{R}_{2}}$=0.6A,
R3、R4并联后电阻为R并=$\frac{{R}_{3}{R}_{4}}{{R}_{3}+{R}_{4}}$=2Ω,再与R1串联后总电阻为R串=R1+R并=10Ω+2Ω=12Ω,此时这段电路的电流为I1=$\frac{U}{{R}_{串}}=\frac{2.4}{12}$=0.2A,
所以通过通过R1的电流为0.2A,R3两端的电压为U3=I1R并=0.2A×2Ω=0.4V,通过R3的电流为I3=$\frac{{U}_{3}}{{R}_{3}}=\frac{0.4}{6}$=0.067A
所以电流表的示数为I=I2+I3=0.6A+0.067A=0.667A.
故答案为:1.8,0.67
点评 本题考查电流表和电压表的读数,关键在于欧姆定律及其变形的灵活运用,难点是明白换接不同的电表时电路的连接,能画出等效电路图,还要知道串、并联电路电流、电压和电阻的规律.

 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案| A. | 推力最小值为Gtanθ | |
| B. | 推力最小值为Gsinθ | |
| C. | 推力最大值为$\frac{G}{cosθ}$ | |
| D. | 推力必须沿斜面向上才能使小球静止 |
| A. | 甲、乙两球间的距离越来越大,两球速度之差越来越大 | |
| B. | 甲、乙两球间的距离越来越大,两球速度之差保持不变 | |
| C. | 甲、乙两球间的距离始终保持不变,两球速度之差保持不变 | |
| D. | 甲、乙两球间的距离越来越小,两球速度之差越来越小 |
 空间某一静电场的电势φ在x轴上分布如图所示,x轴上两点B、C点电场强度在x方向上的分量分别是EBx、ECx,下列说法中正确的有( )
空间某一静电场的电势φ在x轴上分布如图所示,x轴上两点B、C点电场强度在x方向上的分量分别是EBx、ECx,下列说法中正确的有( )| A. | EBx的方向沿x轴正方向 | |
| B. | EBx的大小大于ECx的大小 | |
| C. | 电荷在O点受到的电场力在x方向上的分量最大 | |
| D. | 负电荷沿x轴从B移到C的过程中,电场力先做正功,后做负功 |
| A. | 同一列声波在各种介质中的波长是相同的 | |
| B. | 声波的频率越高,它在空气中传播的速度越快 | |
| C. | 人能辨别不同乐器同时发出的声音,证明声波不会发生干涉 | |
| D. | 声波可以绕过障碍物传播,即它可以发生衍射 |
 如图(a),一物块在t=0时刻滑上一固定斜面,其运动的v?t图线如图(b)所示.若重力加速度及图中的v0、v1、t1均为己知量,则不可求出( )
如图(a),一物块在t=0时刻滑上一固定斜面,其运动的v?t图线如图(b)所示.若重力加速度及图中的v0、v1、t1均为己知量,则不可求出( )| A. | 斜面的倾角 | B. | 物块的质量 | ||
| C. | 物块与斜面间的动摩擦因数 | D. | 物块沿斜面向上滑行的最大高度 |
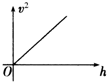
 如图所示,小球从一个固定的光滑的斜槽轨道顶端无初速开始下滑,用v、t和h分别表示小球沿轨道下滑的速度、时间和竖直高度.下列v-t图象和v2-h图象中可能正确的是( )
如图所示,小球从一个固定的光滑的斜槽轨道顶端无初速开始下滑,用v、t和h分别表示小球沿轨道下滑的速度、时间和竖直高度.下列v-t图象和v2-h图象中可能正确的是( )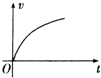


 如图所示,两个长均为L的轻质杆,通过A、B、C上垂直纸面的转动轴与A、B、C三个物块相连,整体处于竖直面内.A、C为两个完全相同的小物块,B物块的质量与A小物块的质量之比为2:1,三个物块的大小都可忽略不计.A、C两物块分别带有+q、-q的电荷量,并置于绝缘水平面上,在水平面上方有水平向右的匀强电场,场强为E,物块间的库仑力不计.当AB、BC与水平面间的夹角均为53°时,整体恰好处于静止状态,一切摩擦均不计,并且在运动过程中无内能产生,重力加速度为g,(sin53°=0.8,cos53°=0.6),则B物块的质量为$\frac{8Eq}{3g}$;若将B物块略向下移动一些,并由静止释放,则B物块到达地面前瞬时速度的大小为$\sqrt{gL}$.
如图所示,两个长均为L的轻质杆,通过A、B、C上垂直纸面的转动轴与A、B、C三个物块相连,整体处于竖直面内.A、C为两个完全相同的小物块,B物块的质量与A小物块的质量之比为2:1,三个物块的大小都可忽略不计.A、C两物块分别带有+q、-q的电荷量,并置于绝缘水平面上,在水平面上方有水平向右的匀强电场,场强为E,物块间的库仑力不计.当AB、BC与水平面间的夹角均为53°时,整体恰好处于静止状态,一切摩擦均不计,并且在运动过程中无内能产生,重力加速度为g,(sin53°=0.8,cos53°=0.6),则B物块的质量为$\frac{8Eq}{3g}$;若将B物块略向下移动一些,并由静止释放,则B物块到达地面前瞬时速度的大小为$\sqrt{gL}$.