题目内容
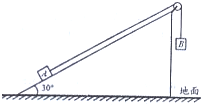 如图所示,水平桌面上固定一楔形木块,其斜面的倾角θ=30°,另一面与水平地面垂直,顶上固定一个定滑轮.跨过定滑轮的细线两端分别与物块A和B连接,A质量为m,B的质量为2m.开始时,将B托在手中不动,细线保持竖直拉紧,然后放开手.当物块B竖直下落距离s后,细线突然断了,此时物块B还没有接触地面.所有摩擦均忽略不计.求:
如图所示,水平桌面上固定一楔形木块,其斜面的倾角θ=30°,另一面与水平地面垂直,顶上固定一个定滑轮.跨过定滑轮的细线两端分别与物块A和B连接,A质量为m,B的质量为2m.开始时,将B托在手中不动,细线保持竖直拉紧,然后放开手.当物块B竖直下落距离s后,细线突然断了,此时物块B还没有接触地面.所有摩擦均忽略不计.求:(1)线断瞬间物块B的速度.
(2)线断后,物块A又沿斜面上滑的最大距离(设A不会与定滑轮相碰).
分析:(1)A、B组成的系统在运动的过程中,只有重力做功,系统机械能守恒,根据机械能守恒定律求出线断瞬间物块B的速度.
(2)线断后,A物体机械能守恒,当A的速度为零时,上滑的距离最大,根据机械能守恒定律求出A上滑的最大距离.
(2)线断后,A物体机械能守恒,当A的速度为零时,上滑的距离最大,根据机械能守恒定律求出A上滑的最大距离.
解答:解:(1)设细线断裂瞬间A和B速度的大小为v,由机械能守恒定律得:
2mgs=mgssin30°+
mv2+
?2mv2
解得v=
.
(2)设物块A继续上滑的距离为s′,由机械能守恒定律得:
mgs′sin30°=
mv2
解得s′=s.
答:(1)线断瞬间物块B的速度为
.
(2)线断后,物块A又沿斜面上滑的最大距离为s.
2mgs=mgssin30°+
| 1 |
| 2 |
| 1 |
| 2 |
解得v=
| gs |
(2)设物块A继续上滑的距离为s′,由机械能守恒定律得:
mgs′sin30°=
| 1 |
| 2 |
解得s′=s.
答:(1)线断瞬间物块B的速度为
| gs |
(2)线断后,物块A又沿斜面上滑的最大距离为s.
点评:解决本题的关键知道绳子未断时,对于单个物体机械能不守恒,因为除重力做功外,还有拉力做功,对系统而言,只有重力做功,机械能守恒.

练习册系列答案
相关题目
 如图所示,水平桌面上的A点处有一个质量为m的物体以初速度v0被抛出,不计空气阻力,当它到达B点时,以地面为零势能面,其机械能的表达式正确的是( )
如图所示,水平桌面上的A点处有一个质量为m的物体以初速度v0被抛出,不计空气阻力,当它到达B点时,以地面为零势能面,其机械能的表达式正确的是( )A、
| ||||
B、
| ||||
| C、mgH-mgh | ||||
D、
|
如图所示,水平桌面上的A点处有一个质量为m的物体以初速度v0被抛出,不计空气阻力,当它到达B点时,其动能的表达式正确的是( ) 
A. | B. |
| C.mgH-mgh | D. |





 B.
B.


 B.
B.
