题目内容
如图所示，物块A的质量m＝2 kg（可看着质点）；木板B的质量M＝3 kg、长L＝1 m。开始时两物体均静止，且A在B最右端，现用F＝24 N的水平拉力拉着轻质滑轮水平向左运动，经过一段时间，物块A滑到木板最左端，不计一切摩擦，求：
(1)此时物块A的速度.
(2)这个过程中拉力F做的功.
(1)此时物块A的速度.
(2)这个过程中拉力F做的功.
(1) 4 m/s. (2) 60 J.
(1)如图乙所示，用F＝24 N的力拉动滑轮时，A、B受到向左的拉力均为F′＝12 N
由牛顿第二定律知：aA＝
＝6 m/s2
aB＝
＝4 m/s2
当A滑到木板左端时，有：
aAt2－aBt2＝L
解得：t＝1 s
此时vA＝aAt＝6 m/s
vB＝aBt＝4 m/s.
(2)解法一 由功能关系知，拉力F做的功等于A、B机械能的增量.
WF＝mv
＋Mv
＝60 J.
解法二 A滑到B左端时，B的位移为：
sB＝aBt2＝2 m
故动滑轮的位移s＝sB＋
＝2.5 m
拉力做的功WF＝F·s＝60 J.
本题考查对牛顿第二定律的而应用，以A为研究对象分析受力可知加速度a，再由运动学公式，两物体的相对位移为L可求出运动时间，由功能关系可知拉力F做功等于系统机械能的增量
由牛顿第二定律知：aA＝
＝6 m/s2aB＝
＝4 m/s2当A滑到木板左端时，有：
aAt2－aBt2＝L解得：t＝1 s
此时vA＝aAt＝6 m/s
vB＝aBt＝4 m/s.
(2)解法一 由功能关系知，拉力F做的功等于A、B机械能的增量.
WF＝
mv＋Mv＝60 J.解法二 A滑到B左端时，B的位移为：
sB＝
aBt2＝2 m故动滑轮的位移s＝sB＋
＝2.5 m拉力做的功WF＝F·s＝60 J.
本题考查对牛顿第二定律的而应用，以A为研究对象分析受力可知加速度a，再由运动学公式，两物体的相对位移为L可求出运动时间，由功能关系可知拉力F做功等于系统机械能的增量
练习册系列答案
相关题目
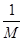的图线
与
，A、B之间的动摩擦因数为
（最大静摩擦力等于滑动摩擦力），一劲度系数为k的轻质弹簧一端固定，另一端与 B相连，在弹性限度范围内，A和 B一起在光滑水平面上作往复运动（不计空气阻力），并保持相对静止。则下列说法正确的是 （ ）
