题目内容
20.已知地球质量大约是月球质量的81倍,地球半径大约是月球半径的4倍.不考虑地球、月球自转的影响,由以上数据可推算出( )| A. | 地球的平均密度与月球的平均密度之比约为9:8 | |
| B. | 地球表面重力加速度与月球表面重力加速度之比约为81:16 | |
| C. | 靠近地球表面沿圆轨道运行的航天器的周期与靠近月球表面沿圆轨道运行的航天器的周期之比约为8:9 | |
| D. | 地球的第一宇宙速度与月球的第一宇宙速度之比为81:4 |
分析 根据质量之比和体积之比求出平均密度之比.根据万有引力等于重力,结合地球和月球的半径之比和质量之比求出表面的重力加速度之比.根据万有引力提供向心力得出周期之比、第一宇宙速度之比.
解答 解:A、根据$ρ=\frac{M}{V}=\frac{M}{\frac{4π{R}^{3}}{3}}$,因为地球质量与月球质量之比为81:1,半径之比为4:1,则体积之比64:1,可知地球的平均密度和月球的平均密度之比为81:64,故A错误.
B、根据$G\frac{Mm}{{R}^{2}}=mg$得,表面的重力加速度g=$\frac{GM}{{R}^{2}}$,因为地球质量与月球质量之比为81:1,半径之比为4:1,则地球表面重力加速度与月球表面重力加速度之比约为81:16,故B正确.
C、根据$G\frac{Mm}{{R}^{2}}=mR\frac{4{π}^{2}}{{T}^{2}}$得,周期T=$\sqrt{\frac{4{π}^{2}{R}^{3}}{GM}}$,因为半径之比为4:1,质量之比为81:1,则靠近地球表面沿圆轨道运行的航天器的周期与靠近月球表面沿圆轨道运行的航天器的周期之比约为8:9,故C正确.
D、根据$G\frac{Mm}{{R}^{2}}=m\frac{{v}^{2}}{R}$得,第一宇宙速度v=$\sqrt{\frac{GM}{R}}$,因为半径之比为4:1,质量之比为81:1,则地球的第一宇宙速度与月球的第一宇宙速度之比为9:2.故D错误.
故选:BC.
点评 解决本题的关键掌握万有引力定律的两个重要理论:1、万有引力等于重力,2、万有引力提供向心力,并能灵活运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19. 如图所示,一质量为m的木块P靠在粗糙竖直的墙壁上,木块与墙壁间的动摩擦系数为μ,且受到水平力F的作用,下列说法正确的是( )
如图所示,一质量为m的木块P靠在粗糙竖直的墙壁上,木块与墙壁间的动摩擦系数为μ,且受到水平力F的作用,下列说法正确的是( )
 如图所示,一质量为m的木块P靠在粗糙竖直的墙壁上,木块与墙壁间的动摩擦系数为μ,且受到水平力F的作用,下列说法正确的是( )
如图所示,一质量为m的木块P靠在粗糙竖直的墙壁上,木块与墙壁间的动摩擦系数为μ,且受到水平力F的作用,下列说法正确的是( )| A. | 若木块静止,则木块P受到的静摩擦力大小等于mg,方向竖直向上 | |
| B. | 若木块静止,当F增大时,木块P受到的静摩擦力随之增大 | |
| C. | 若撤去F后木块沿墙壁下滑时,木块不受滑动摩擦力作用 | |
| D. | 保持F不变,在P上放另一物体,若木块P仍静止,则P受到的摩擦力大小不变 |
20.下列说法正确的是( )
| A. | 速度是描述物体位置变化的物理量 | |
| B. | 静止的物体可能受到滑动摩擦力,运动的物体可能受到静摩擦力 | |
| C. | 物体受到滑动摩擦力的方向一定与物体运动方向相反 | |
| D. | 物体受到摩擦力的大小一定与物体与接触面之间的弹力大小成正比 |
10.如图所示,一木块受到垂直于倾斜墙面方向的推力F作用而处于静止状态,下列判断正确的是( )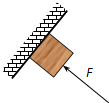

| A. | 墙面与木块间的弹力可能为零 | |
| B. | 墙面对木块的摩擦力方向沿倾斜墙面向上 | |
| C. | 在推力F逐渐增大过程中,木块将始终维持静止状态 | |
| D. | 在推力F逐渐增大过程中,木块所受墙面的摩擦力始终不变 |
 在坐标系xOy中,有三个靠在一起的等大的圆形区域,分别存在着方向如图所示的匀强磁场,磁感应强度大小都为B=0.10T,磁场区域半径r=$\frac{2\sqrt{3}}{3}$m,三个圆心A、B、C构成一个等边三角形,B、C点都在x轴上,且y轴与圆形圆域C相切,圆形区域A内磁场垂直纸面向里,圆形区域B、C内磁场垂直纸面向外.在直角坐标系的第Ⅰ、Ⅳ象限内分布着场强E=1.0×105N/C的竖直方向的匀强电场,现有质量m=3.2×10-26kg,带电荷量q=-1.6×10-19C的某种负离子,从圆形磁场区域A的左侧边缘以水平速度v=106m/s沿正对圆心A的方向垂直磁场射入,求:
在坐标系xOy中,有三个靠在一起的等大的圆形区域,分别存在着方向如图所示的匀强磁场,磁感应强度大小都为B=0.10T,磁场区域半径r=$\frac{2\sqrt{3}}{3}$m,三个圆心A、B、C构成一个等边三角形,B、C点都在x轴上,且y轴与圆形圆域C相切,圆形区域A内磁场垂直纸面向里,圆形区域B、C内磁场垂直纸面向外.在直角坐标系的第Ⅰ、Ⅳ象限内分布着场强E=1.0×105N/C的竖直方向的匀强电场,现有质量m=3.2×10-26kg,带电荷量q=-1.6×10-19C的某种负离子,从圆形磁场区域A的左侧边缘以水平速度v=106m/s沿正对圆心A的方向垂直磁场射入,求:
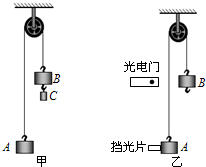 如图甲所示的装置叫做阿特伍德机,是英国数学家和物理学家阿特伍德(G•Atwood 1746-1807)创制的一种著名力学实验装置,用来研究匀变速直线运动的规律.某同学对该装置加以改进后用来验证机械能守恒定律,如图乙所示.
如图甲所示的装置叫做阿特伍德机,是英国数学家和物理学家阿特伍德(G•Atwood 1746-1807)创制的一种著名力学实验装置,用来研究匀变速直线运动的规律.某同学对该装置加以改进后用来验证机械能守恒定律,如图乙所示.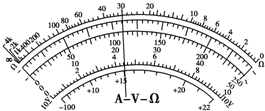 (1)用多用表的欧姆挡测量阻值约为几千欧的电阻Rx,以下给出的是可能的实验操作步骤,其中S为选择开关,P为欧姆挡调零旋钮.把你认为正确步骤前的字母按合理的顺序填写在下面的横线上.
(1)用多用表的欧姆挡测量阻值约为几千欧的电阻Rx,以下给出的是可能的实验操作步骤,其中S为选择开关,P为欧姆挡调零旋钮.把你认为正确步骤前的字母按合理的顺序填写在下面的横线上.