题目内容
3. 如图所示,质量为m1=0.2kg,大小可忽略不计的物块A以V1=3m/s的速度水平向右滑上质量为m2=0.1kg的木板B的左端,同时木板B以V2=1m/s水平向左运动,AB间动摩擦因数μ=0.5,水平面光滑,木板B的长度L=0.5m,g=10m/s2.求:从物块A滑上木板B至滑离木板B的过程中A对B的冲量大小.
如图所示,质量为m1=0.2kg,大小可忽略不计的物块A以V1=3m/s的速度水平向右滑上质量为m2=0.1kg的木板B的左端,同时木板B以V2=1m/s水平向左运动,AB间动摩擦因数μ=0.5,水平面光滑,木板B的长度L=0.5m,g=10m/s2.求:从物块A滑上木板B至滑离木板B的过程中A对B的冲量大小.
分析 物块A滑上木板B至滑离木板B的过程中,根据系统动量守恒和能量守恒列车等式求出滑离的末速度,
根据动量定理得出A对B的冲量大小.
解答 解:物块A滑上木板B至滑离木板B的过程中,规定向右为正方向,
根据系统动量守恒得
m1v1-m2v2=m1v′1+m2v′2
根据能量守恒得
μm1gL=$\frac{1}{2}$m1${v}_{1}^{2}$+$\frac{1}{2}$m2${v}_{2}^{2}$-$\frac{1}{2}$m1${v′}_{1}^{2}$-$\frac{1}{2}$m2${v′}_{2}^{2}$
解得:v′1=2m/s,v′2=1m/s
根据动量定理得出A对B的冲量大小I=0.1×1-0.1×(-1)=0.2N•S.
答:从物块A滑上木板B至滑离木板B的过程中A对B的冲量大小是0.2N•S.
点评 本题考查了求速度与冲量问题,分析清楚运动过程、选择恰当的过程应用动量守恒定律、能量守恒定律、动量定理即可正确解题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11. 空间某区域竖直平面内存在电场,电场线分布如图所示.一个质量为m、电量为q,电性未知的小球在该电场中运动,小球经过A点时的速度大小为v1,方向水平向右,运动至B点时的速度大小为v2.若A、B两点之间的高度差为h,则以下判断中正确的是( )
空间某区域竖直平面内存在电场,电场线分布如图所示.一个质量为m、电量为q,电性未知的小球在该电场中运动,小球经过A点时的速度大小为v1,方向水平向右,运动至B点时的速度大小为v2.若A、B两点之间的高度差为h,则以下判断中正确的是( )
 空间某区域竖直平面内存在电场,电场线分布如图所示.一个质量为m、电量为q,电性未知的小球在该电场中运动,小球经过A点时的速度大小为v1,方向水平向右,运动至B点时的速度大小为v2.若A、B两点之间的高度差为h,则以下判断中正确的是( )
空间某区域竖直平面内存在电场,电场线分布如图所示.一个质量为m、电量为q,电性未知的小球在该电场中运动,小球经过A点时的速度大小为v1,方向水平向右,运动至B点时的速度大小为v2.若A、B两点之间的高度差为h,则以下判断中正确的是( )| A. | A、B两点的电场强度和电势大小关系为EA>EB、φA<φB | |
| B. | 若v2>v1,则电场力一定做正功 | |
| C. | A、B两点间的电势差为$\frac{m}{2q}$(v22-v12-2gh) | |
| D. | 小球从A运动到B点的过程中电场力做的功为$\frac{1}{2}$mv22-$\frac{1}{2}$mv12 |
18.下列关于分子运动和热现象的说法正确的是( )
| A. | 气体如果失去了容器的约束就会散开,这是因为气体分子之间存在势能的缘故 | |
| B. | 一定量100℃的水变成100℃的水蒸气,其分子之间的势能增加 | |
| C. | 对于一定量的气体,如果压强不变,体积增大,那么它一定从外界吸热 | |
| D. | 如果气体分子总数不变,而气体温度升高,气体分子的平均动能增大,因此压强必然增大 | |
| E. | 一定量气体的内能等于其所有分子热运动动能和分子之间势能的总和 |
8. 如图所示,物体A、B的质量分别为M和m,A物体在水平桌面上,两者通过光滑小滑轮用轻绳相连.释放物体A,在A向右运动的过程中,其加速度为a1,绳中张力为F1.现将物体A重新拉回释放点,并将B物用竖直向下的力F=mg代替,在A再向右运动的过程中,其加速度为a2,绳中张力为F2,则( )
如图所示,物体A、B的质量分别为M和m,A物体在水平桌面上,两者通过光滑小滑轮用轻绳相连.释放物体A,在A向右运动的过程中,其加速度为a1,绳中张力为F1.现将物体A重新拉回释放点,并将B物用竖直向下的力F=mg代替,在A再向右运动的过程中,其加速度为a2,绳中张力为F2,则( )
 如图所示,物体A、B的质量分别为M和m,A物体在水平桌面上,两者通过光滑小滑轮用轻绳相连.释放物体A,在A向右运动的过程中,其加速度为a1,绳中张力为F1.现将物体A重新拉回释放点,并将B物用竖直向下的力F=mg代替,在A再向右运动的过程中,其加速度为a2,绳中张力为F2,则( )
如图所示,物体A、B的质量分别为M和m,A物体在水平桌面上,两者通过光滑小滑轮用轻绳相连.释放物体A,在A向右运动的过程中,其加速度为a1,绳中张力为F1.现将物体A重新拉回释放点,并将B物用竖直向下的力F=mg代替,在A再向右运动的过程中,其加速度为a2,绳中张力为F2,则( )| A. | a2=a1,F2=F1 | B. | a2>a1,F2>F1 | C. | a2<a1,F2<F1 | D. | a2=a1,F2>F1 |
15. 如图所示,在光滑的水平面上,有一垂直向下的匀强磁场分布在宽为L的区域内,有一个边长为a(a<L)的正方形闭合线圈以初速v0垂直磁场边界滑过磁场后速度变为v(v<v0),则( )
如图所示,在光滑的水平面上,有一垂直向下的匀强磁场分布在宽为L的区域内,有一个边长为a(a<L)的正方形闭合线圈以初速v0垂直磁场边界滑过磁场后速度变为v(v<v0),则( )
 如图所示,在光滑的水平面上,有一垂直向下的匀强磁场分布在宽为L的区域内,有一个边长为a(a<L)的正方形闭合线圈以初速v0垂直磁场边界滑过磁场后速度变为v(v<v0),则( )
如图所示,在光滑的水平面上,有一垂直向下的匀强磁场分布在宽为L的区域内,有一个边长为a(a<L)的正方形闭合线圈以初速v0垂直磁场边界滑过磁场后速度变为v(v<v0),则( )| A. | 完全进入磁场中时线圈的速度大于$\frac{{v}_{0}+v}{2}$ | |
| B. | 安全进入磁场中时线圈的速度等于$\frac{{v}_{0}+v}{2}$ | |
| C. | 完全进入磁场中时线圈的速度小于$\frac{{v}_{0}+v}{2}$ | |
| D. | 以上情况A、B均有可能,而C是不可能的 |
12.关于原子和原子核,下列说法中正确的是( )
| A. | 卢瑟福根据α散射的实验结果,提出了原子的核式结构模型 | |
| B. | 根据爱因斯坦的质能方程,可求出原子核的结合能 | |
| C. | 氕、氘、氚核中具有相同的中子数和不同的核子数,所以是氢的同位素 | |
| D. | 氢原子吸收一个光子从低能级跃迁到高能级,氢原子的动能增加了 |
 如图所示,U型金属框架质量m2=0.2kg,放在绝缘水平面上,与水平面间的动摩擦因数μ=0.2,MM′、NN′相互平行且相距0.4m,电阻不计,且足够长,MN段垂直于MM′,电阻R2=0.1Ω.光滑导体棒ab垂直横放在U型金属框架上,其质量m1=0.1kg、电阻R1=0.3Ω、长度l=0.4m.整个装置处于竖直向上的匀强磁场中,磁感应强度B=0.5T.现垂直于ab棒施加F=2N的水平恒力,使ab棒从静止开始运动,且始终与MM′、NN′保持良好接触,当ab棒运动到某处时,框架开始运动.设框架与水平面间最大静摩擦力等于滑动摩擦力,g取10m/s2.
如图所示,U型金属框架质量m2=0.2kg,放在绝缘水平面上,与水平面间的动摩擦因数μ=0.2,MM′、NN′相互平行且相距0.4m,电阻不计,且足够长,MN段垂直于MM′,电阻R2=0.1Ω.光滑导体棒ab垂直横放在U型金属框架上,其质量m1=0.1kg、电阻R1=0.3Ω、长度l=0.4m.整个装置处于竖直向上的匀强磁场中,磁感应强度B=0.5T.现垂直于ab棒施加F=2N的水平恒力,使ab棒从静止开始运动,且始终与MM′、NN′保持良好接触,当ab棒运动到某处时,框架开始运动.设框架与水平面间最大静摩擦力等于滑动摩擦力,g取10m/s2.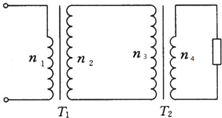 有一台发电机通过升压和降压变压器给用户供电.已知发电机的输出电功率为500kW,端电压为500V,升压变压器原、副线圈的匝数比是1:5,两变压器之间输电导线的总电阻是1.5Ω,降压变压器的输出电压是220V.求:
有一台发电机通过升压和降压变压器给用户供电.已知发电机的输出电功率为500kW,端电压为500V,升压变压器原、副线圈的匝数比是1:5,两变压器之间输电导线的总电阻是1.5Ω,降压变压器的输出电压是220V.求: