题目内容
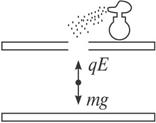
如图所示,一个带电小球用绝缘细线悬挂在匀强电场中,当悬线与竖直方向成60°角时,球恰好处于平衡状态,若线长为0.05m,小球质量为0.1kg,电场强度为(1)两金属板的电势差U=_____MV.
(2)小球的电荷量q=_______μC.
(3)如果将小球在A点由静止释放,那么它到达B点时的速度为_______m/s.

答案:0.1;1;1
解析:
解析:
|
解: 1)U= Ed= 105V. 2)由共点力平衡条件得 qE= mgtg60°. 所以q= (mg/E)tg60°= 1.0 ×10-6C. 3)由动能定理得 qELsin60°- mg(L- Lcos60°)= (1/2)mv2- 0,
所以v= = 1m/s. |

练习册系列答案
 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
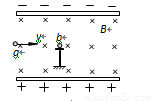
 如图所示,带电平行金属板相互正对水平放置,两板间存在着水平方向的匀强磁场.带电液滴a沿垂直于电场和磁场的方向进入板间后恰好沿水平方向做直线运动,在它正前方有一个静止在小绝缘支架上不带电的液滴b.带电液滴a与液滴b发生正碰,在极短的时间内复合在一走形成带电液滴c,若不计支架对液滴c沿水平方向的作用力,则液滴离开支架后( )
如图所示,带电平行金属板相互正对水平放置,两板间存在着水平方向的匀强磁场.带电液滴a沿垂直于电场和磁场的方向进入板间后恰好沿水平方向做直线运动,在它正前方有一个静止在小绝缘支架上不带电的液滴b.带电液滴a与液滴b发生正碰,在极短的时间内复合在一走形成带电液滴c,若不计支架对液滴c沿水平方向的作用力,则液滴离开支架后( )| A、一定做曲线运动 | B、可能做直线运动 | C、可能做匀速圆周运动 | D、电场力对它做正功 |
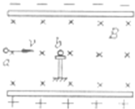
如图所示,带电平行金属板相互正对水平放置,两板间存在着水平方向的匀强磁场。带电液滴a沿垂直于电场和磁场的方向进入板间后恰好沿水平方向做直线运动,在它正前方有一个静止在小绝缘支架上不带电的液滴b。带电液滴a与液滴b发生正碰,在极短的时间内复合在一起形成带电液滴c,若不计支架对液滴c沿水平方向的作用力,则液滴离开支架后 ( )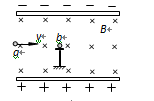
| A.液滴一定带正电 | B.一定做直线运动 |
| C.一定做匀速圆周运动 | D.一定做匀变速曲线运动 |