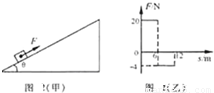
题目内容
半径R=4500km的某星球上有一倾角为30°的固定斜面，一质量为1kg的小物块在力F作用下从静止开始沿斜面向上运动，力F始终与斜面平行．如果物块和斜面间的摩擦因数μ=
| ||
| 3 |
（1）该星球的质量大约是多少？
（2）要从该星球上抛出一个物体，使该物体不再落回星球，至少需要多大速度？（计算结果保留二位有效数字）
分析：（1）由图可知，读出力的大小的大小．分前后两个1s时间进行研究，根据牛顿第二定律和运动学公式列方程联立解出重力加速度；物体在星球上，重力等于万有引力，列式求出该星球的质量．
（2）要使该物体不再落回星球，必须使重力提供向心力，根据牛顿第二定律求出最小的速度．
（2）要使该物体不再落回星球，必须使重力提供向心力，根据牛顿第二定律求出最小的速度．
解答：解：（1）设星球表面的重力加速度为g．
小物块在力F1=20N作用过程中有：F1-mgsinθ-μmgcosθ=ma1
1s末速度为 v=a1t1
小物块在力F2=4N作用过程中有：F2+mgsinθ+μmgcosθ=ma2
且有 v=a2t2
联立以上四式，解得 g=8m/s2
由G
=mg
得 M=
=
kg=2.4×1024kg
（2）要从该星球上抛出一个物体，使该物体不再落回星球，物体的最小速度为v′，必须满足：mg=m
得v′=
=
=6×103m/=6.0km/s
答：
（1）该星球的质量大约是2.4×1024kg．
（2）要从该星球上抛出一个物体，使该物体不再落回星球，至少需要6.0km/s的速度．
小物块在力F1=20N作用过程中有：F1-mgsinθ-μmgcosθ=ma1
1s末速度为 v=a1t1
小物块在力F2=4N作用过程中有：F2+mgsinθ+μmgcosθ=ma2
且有 v=a2t2
联立以上四式，解得 g=8m/s2
由G
| Mm |
| R2 |
得 M=
| gR2 |
| G |
| 8×(4500×103)2 |
| 6.67×10-11 |
（2）要从该星球上抛出一个物体，使该物体不再落回星球，物体的最小速度为v′，必须满足：mg=m
| v′2 |
| R |
得v′=
| gR |
| 8×4500×103 |
答：
（1）该星球的质量大约是2.4×1024kg．
（2）要从该星球上抛出一个物体，使该物体不再落回星球，至少需要6.0km/s的速度．
点评：本题是万有引力定律与牛顿定律的综合应用，第二题，由重力或万有引力提供向心力，求出该星球的第一宇宙速度．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
目标测试系列答案
相关题目
（2012?东至县模拟）半径R=4500km的某星球上有一倾角为θ=30°的固定斜面．一质量为m=1lg的小物块在力F作用下从静止开始沿斜面向上运动，力F始终与斜面平行，如图12（甲）所示．已知小物块和斜面间的动摩擦因数
，力F随时间变化的规律如图所示（取沿斜面向上方向为正），2s末物块速度恰好又为0．引力恒量G=6.67×10-11Nm2/kg2．试求：
，力F随时间变化的规律如图所示（取沿斜面向上方向为正），2s末物块速度恰好又为0．引力恒量G=6.67×10-11Nm2/kg2．试求：
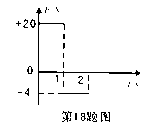
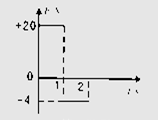
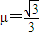，力F随位移s变化的规律如图（乙）所示（取沿斜面向上的方向为正），那么小物块运动12m时速度恰好为零．试求：