题目内容
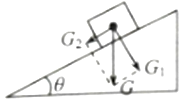
【题目】如图所示，半径为R、圆心为O的大圆环固定在竖直平面内，两个轻质小圆环固定在大圆环上竖直对称轴的两侧θ=45°的位置上，一根轻质长绳穿过两个小圆环，它的两端都系上质量为m的重物，小圆环的大小、绳子与大、小圆环间的摩擦均可忽略．当在两个小圆环间绳子的中点C处，挂上一个质量M的重物，M恰好在圆心处处于平衡．（重力加速度为g）求：
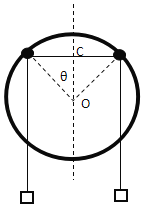
（1）M与m质量之比．
（2）再将重物M托到绳子的水平中点C处，然后无初速释放重物M，则重物M到达圆心处的速度是多大？
【答案】（1）
（2）
【解析】(1)以M为研究对象，受力分析：Mg=2mgcos450
(2)M与2个m组成的系统机械能守恒：
MgRsinθ-2mg(R-Rcosθ)= 
MV12+
mV22
V2=V1cosθ
口算心算速算应用题系列答案
同步拓展阅读系列答案【题目】甲乙两位同学利用穿过打点计时器的纸带来记录小车的运动，打点计时器所用电源的频率为50Hz．
（1）实验后，甲同学选择了一条较为理想的纸带，测量数据后，通过计算得到了小车运动过程中各计时时刻的速度如表格所示．
位置编号 | 0 | 1 | 2 | 3 | 4 | 5 |
时间：t/s | 0 | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 |
速度：v/ms﹣1 | 0.42 | 0.67 | 0.92 | 1.16 | 1.42 | 1.76 |
分析表中数据，在误差允许的范围内，小车做运动；由于此次实验的原始纸带没有保存，该同学想估算小车从位置0到位置5的位移，其估计算方法如下：x=（0.42×0.1+0.67×0.1+0.92×0.1+1.16×0.1+1.42×0.1）m，那么，该同学得到的位移 （选填“大于”、“等于”或“小于”）实际位移．
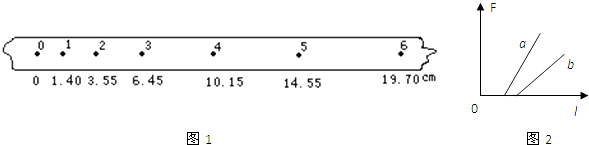
（2）乙同学的纸带如图1，按时间顺序取0、1、2、3、4、5、6七个计数点，每相邻的两计数点间都有四个点未画出．用刻度尺量出1、2、3、4、5、6点到0点的距离如图2所示（单位：cm）．由纸带数据计算可得计数点3所代表时刻的瞬时速度大小v3=m/s，小车的加速度大小a=m/s2 ． 
