题目内容
8. 如图所示,在光滑绝缘水平面上,有一质量不计的绝缘木板长3m,下表面光滑,上表面粗糙.其上放有带电滑块甲和乙,甲的质量为m1=4×10-3 kg,乙的质量为m2=2×10-3 kg,甲带正电其电荷量q1为4×10-5 C,乙带负电其电荷量q2为2×10-5 C.甲乙两滑块和木板间的动摩擦因数均为0.1.开始时甲、乙两滑块距木板左、右边缘均为1m,现突然在整个装置周围加上空间足够大的、方向水平向右的匀强电场,不计滑块间的库仑力,试求:
如图所示,在光滑绝缘水平面上,有一质量不计的绝缘木板长3m,下表面光滑,上表面粗糙.其上放有带电滑块甲和乙,甲的质量为m1=4×10-3 kg,乙的质量为m2=2×10-3 kg,甲带正电其电荷量q1为4×10-5 C,乙带负电其电荷量q2为2×10-5 C.甲乙两滑块和木板间的动摩擦因数均为0.1.开始时甲、乙两滑块距木板左、右边缘均为1m,现突然在整个装置周围加上空间足够大的、方向水平向右的匀强电场,不计滑块间的库仑力,试求:(1)若加上匀强电场后甲和乙都没有脱离木板,求所加电场强度大小的范围.
(2)若所加的电场强度为150N/C,经过多长时间乙从木板上滑下?从加上电场到乙从木板上滑下的过程中,甲和乙电势能总的变化量是多少?
分析 (1)分析甲、乙和木板上静摩擦力大小,分析不脱离木板的临界条件;再对整体受力分析可求得电场强度的范围;
(2)分别对甲乙两物体受力分析,由牛顿第二定律可求得加速度;再由位移公式可求得时间;根据功能关系可求得总的电势能的改变量.
解答 解:(1)乙的最大静摩擦力f2=μm2g=0.1×2×10-3×10=2×10-3N;
甲的最大静摩擦力f1=μm1g=0.1×4×10-3×10=4×10-3N;
f1>f2
故当电场强度增大到一定值时木板跟甲一起运动.
甲和乙不脱离木板的临界条件为乙达到最大静摩擦力
对甲、乙和木板整体水平方向受力分析有:
Eq1-Eq2=(m1+m2)a
对乙水平方向受力分析有:
μm2g-Eq2=m2a
代入数据解得:E=75N/C
故所加电场强度应小于75N/C;
(2)当所加的电场强度为150 N/C时:
对乙受力分析有:Eq2-μm2g=m2a2,
得a2=0.5m/s2;
对甲受力分析有:Eq1-μm2g=m1a1
得a1=1m/s2;
乙由静止到从木板上滑下过程中:
DL=$\frac{1}{2}$a1t2+$\frac{1}{2}$a2t2得
t=$\sqrt{\frac{4}{3}}$s=$\frac{2\sqrt{3}}{3}$s
甲的位移为:x1=$\frac{1}{2}$a1t2=$\frac{2}{3}$m;
甲的电势能减少量
EP1=Eq1x1=4×10-3J;
乙的位移为:x2=$\frac{1}{2}$a2t2=$\frac{1}{3}$m,
乙的电势能减少量Ep2=Eq2x2=1×10-3J;
甲和乙电势能总的变化量是
EP=EP1+EP2=5×10-3J
答:(1)所加电场强度大小的范围应小于75N/C;
(2)甲和乙电势能总的变化量是5×10-3J
点评 本题考查带电粒子在电场中的运动,要注意明确过程分析及受力分析,根据牛顿第二定律和功能关系进行分析求解.

| A. | 81:80 | B. | 9:5 | C. | 5:1 | D. | 10:1 |
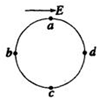 一半径为R的光滑圆环竖直放在水平向右场强为E的匀强电场中,如图所示,环上a、c是竖直直径的两端,b、d是水平直径的两端,质量为m的带电小球套在圆环上,并可沿环无摩擦滑动.现使小球由a点静止释放,沿abc运动到d点时速度恰好为零,由此可知( )
一半径为R的光滑圆环竖直放在水平向右场强为E的匀强电场中,如图所示,环上a、c是竖直直径的两端,b、d是水平直径的两端,质量为m的带电小球套在圆环上,并可沿环无摩擦滑动.现使小球由a点静止释放,沿abc运动到d点时速度恰好为零,由此可知( )| A. | 小球的d点时的加速度为零 | |
| B. | 小球在b点时机械能最大 | |
| C. | 小球在c点时机械能最小,电势能最大 | |
| D. | 小球在bc之间某点动能最大 |

同学们设计了以下表格来记录实验数据.其中L1、L2、L3、L4…代表物体分别从不同初始位置处无初速释放时初始位置到速度传感器的距离,v1、v2、v3、v4…表示物体每次通过Q点的速度.
| 实验次数 | 1 | 2 | 3 | 4 | … |
| L | L1 | L1 | L3 | L4 | … |
| v | v1 | v2 | v3 | v4 | … |
(1)你认为他们的做法是否合适?不合适
(2)你有什么好的建议?应进一步绘制L-v2 图象
(3)在此实验中,木板与物体间摩擦力的大小不会(填“会”或“不会”)影响探究出的结果.
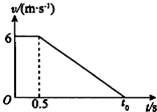 新交规已经正式施行,司机闯黄灯要扣6分,被称为“史上最严交规”.某小轿车驾驶员看到绿灯开始闪时,经短暂思考后开始刹车,小轿车在黄灯刚亮时恰停在停车线上,v-t图线如图所示.若绿灯开始闪烁时小轿车距停车线距离L=10.5m,则绿灯开始闪烁到黄灯刚亮的时间t0为( )
新交规已经正式施行,司机闯黄灯要扣6分,被称为“史上最严交规”.某小轿车驾驶员看到绿灯开始闪时,经短暂思考后开始刹车,小轿车在黄灯刚亮时恰停在停车线上,v-t图线如图所示.若绿灯开始闪烁时小轿车距停车线距离L=10.5m,则绿灯开始闪烁到黄灯刚亮的时间t0为( )| A. | 0.5 s | B. | 1.5 s | C. | 3 s | D. | 3.5 s |
| A. | 竖直向上抛出的物体,物体竖直上升,是因为受到一个竖直向上的升力作用 | |
| B. | 放在斜面上的物体会沿斜面下滑,是因为受到一个下滑力作用 | |
| C. | 放在水中的木块会上浮,是因为受到了浮力的作用 | |
| D. | 运动员跳远,腾空后能前进几米,是因为受到了空气的推力 |